题目内容
小河两岸边各有一棵树,分别高30尺和20尺,两树的距离是50尺,每棵树的树顶上都停着一只鸟.忽然,两只鸟同时看见水面上游出一条鱼,它们立刻飞去抓鱼,速度相同,并且同时到达目标.则这条鱼出现的地方离开比较高的树的距离为______尺.
由题意得:AB=20尺,DC=30尺,BC=50尺,
设EC为x,则BE为(50-x),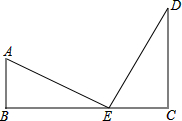
在Rt△ABE中,AE2=AB2+BE2=202+(50-x)2,
在Rt△DEC中,DE2=DC2+EC2=302+x2,
又∵AE=DE,
∴x2+302=(50-x)2+202,
解得:x=20,
即这条鱼出现的地方离比较高的树的距离为20尺.
故答案为:20.
设EC为x,则BE为(50-x),

在Rt△ABE中,AE2=AB2+BE2=202+(50-x)2,
在Rt△DEC中,DE2=DC2+EC2=302+x2,
又∵AE=DE,
∴x2+302=(50-x)2+202,
解得:x=20,
即这条鱼出现的地方离比较高的树的距离为20尺.
故答案为:20.

练习册系列答案
相关题目







