题目内容
已知等腰三角形面积为4
cm2,一腰上的高为2
cm,则这条高与底边的夹角为______.
| 3 |
| 3 |
∵等腰三角形面积为4
cm2,一腰上的高为2
cm,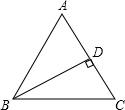
∴
•AC•BD=4
,
∴AC=AB=
=4,
在直角△ABD中,cos∠ABD=
=
=
.
∴∠ABD=30°,
∴AD=sin30°•AB=2,
∴CD=2,
在Rt△BDC中,tan∠DBC=
=
,
∴∠DBC=30°,
∴这条高与底边的夹角为30°,
故答案是:30°.
| 3 |
| 3 |

∴
| 1 |
| 2 |
| 3 |
∴AC=AB=
2×4
| ||
2
|
在直角△ABD中,cos∠ABD=
| BD |
| AB |
2
| ||
| 4 |
| ||
| 2 |
∴∠ABD=30°,
∴AD=sin30°•AB=2,
∴CD=2,
在Rt△BDC中,tan∠DBC=
| DC |
| BD |
| ||
| 3 |
∴∠DBC=30°,
∴这条高与底边的夹角为30°,
故答案是:30°.

练习册系列答案
相关题目






