Question

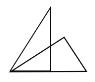
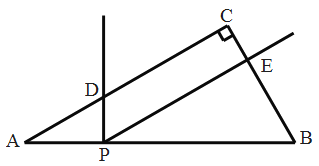
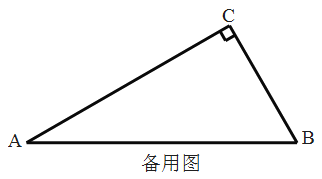
【题目】如图，在△ABC中，∠ACB=90°，∠A=30°，AB=4，点P是AB边上的一个动点。过点P作AB的垂线交AC边于点D，以PD为边作∠DPE=60°，PE交BC边于点E。

（1）以点D为AC边的中点时，求BE的长

（2）当PD=PE时，求AP的长；

（3）设AP的长为x，四边形CDPE的面积为y，求出y与x的函数解析式及自变量的取值范围。

Answer 1

【答案】（1）；（2）；（3），.

【解析】

（1）根据勾股定理可求出AC和BC的长，从而知AD的长度，在中可求出AP的长，则，又因可知，根据直角三角形的性质即可得BE的长；

（2）设，由题（1）可知，在和中可以求出AP和BP的长，再根据求解即可得；

（3）由可得DP、BP的长，从而得BE和EP的长，根据面积公式可列出等式：，化简即可得，最后根据和联立求x的取值范围.

（1）由题意可得，在中，

点D为AC的中点

在中可得，

又

在中，；

（2）设

由题（1）可知，在中，

在中，

又，即

解得

；

（3）设，则

在中，

在中，

即

化简得

由题意得，即

又，即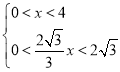

联立解得

故出y与x的函数解析式为，自变量的取值范围为.