题目内容
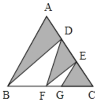
【题目】已知在△ABC中，∠C＝90°，AC＝3，BC＝4，分别以AC、BC、AB为直径作半圆，如图所示，则阴影部分的面积是_____．
【答案】6
【解析】
先利用勾股定理列式求出AB，再根据阴影部分面积等于以AC、BC为直径的两个半圆的面积加上直角三角形ABC的面积减去以AB为直径的半圆的面积，列式计算即可得解．
解：∵在Rt△ABC中，∠ACB＝90°，
∴AC2+ BC2＝AB2，
∵BC＝4，AC＝3，
∴AB＝
＝5，
S阴影＝直径为AC的半圆的面积＋直径为BC的半圆的面积＋S△ABC直径为AB的半圆的面积
＝
π（
）2＋π（
）2＋AC×BCπ（
）2，
＝
π（AC）2＋π（BC）2π（AB）2＋AC×BC，
＝π（AC2+ BC2－AB2）+AC×BC，
＝AC×BC，
=×3×4
＝6．
故答案为：6.
练习册系列答案
相关题目
