题目内容
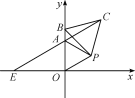
【题目】如图,在平面直角坐标系中,△AOP为等边三角形,A(0,2),点B为y轴上一动点,以BP为边作等边△PBC,延长CA交x轴于点E.
(1)求证:OB=AC;
(2)∠CAP的度数是;
(3)当B点运动时,猜想AE的长度是否发生变化?并说明理由;
(4)在(3)的条件下,在y轴上存在点Q,使得△AEQ为等腰三角形,请写出点Q的坐标.
【答案】(1)答案见解析;(2)答案见解析;(3)答案见解析;(4)答案见解析.
【解析】
(1)根据等边三角形性质得出OP=AP,BP=PC,∠APO=∠CPB=60°,求出∠OPB=∠APC,证出△PBO≌△PCA即可;(2)当点B在y轴正半轴上时,由(1)知∠PBO=∠PCA,根据∠BAC=∠BPC=60°,当点B在y轴负半轴上时,判断出△APC≌△OPB(SAS),即可求出答案;(3)∠EAO=60°,求出∠AEO=30°,得出AE=2AO,求出即可;(4)分点Q在y轴正半轴和负半轴两种情况计算即可.
解:(1)证明:∵△AOP,△PBC均为等边三角形,
∴OP=AP,BP=PC,∠OPA=∠BPC=60°.
∴∠OPA+∠APB=∠APB+BPC,即∠OPB=∠APC.
在△PBO和△PCA中,
∴△PBO≌△PCA(SAS).∴OB=AC.
(2)当点B在y轴正半轴上时,
由(1)知∠PBO=∠PCA,
∴∠BAC=∠BPC=60°,
又∵∠OAP=60°,
∴∠CAP=60°.
当点B在y轴负半轴上时,如图,
∵△AOP和△BCP是等边三角形,
∴AP=OP,PC=PB,∠AOP=∠APO=∠BPC=60°,
∴∠APC=∠OPB,
∴△APC≌△OPB(SAS),
∴∠CAP=∠BOP=180°-∠AOP=120°,
∵延长CA交x轴于点E,
∴此种情况不符合题意,舍去,
故∠CAP的度数是60°;
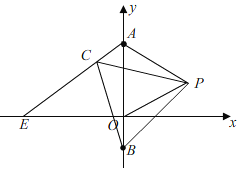
(3)当点B运动时,AE的长度不会发生变化.理由如下:
∵∠CAP=60°,∠PAO=60°,
∴∠EAO=180°-60°-60°=60°.
∵∠AOE=90°,∴∠AEO=30°.∴AE=2AO.
∵A(0,2),∴OA=2.∴AE=4.
∴当B点运动时,AE的长度不发生变化,为4.
(4) 由(3)知,AE=4,∠OAE=60°,
当点Q在y轴负半轴时,
∵OA⊥AE,
∴点Q与点A关于x轴对称,
∴Q(0,-2),
当点Q在y轴正半轴时,EQ=AE=4,
∴OQ=OA+EQ=6,
∴Q(0,6).
即:满足条件的点Q的坐标为(0,-2)或(0,6).

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案