题目内容
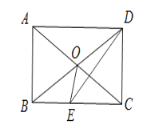
【题目】如图,在矩形ABCD中,对角线AC、BD交于点O,DE平分∠ADC.若∠AOB=60°,则∠COE的大小为____ .
【答案】75°
【解析】
根据四边形ABCD为矩形,利用矩形的对角线互相平分且相等,得到OA=OB=OC=OD,又∠AOB=60°,可得三角形AOB与三角形COD都为等边三角形,进而求出∠ACB为30°,由DE为直角的角平分线,得到∠EDC=45°,可得三角形DEC为等腰直角三角形,即CD=EC,而CD=OC,等量代换可得EC=OC,即三角形OEC为等腰三角形,由顶角∠ACB为30°即可求出底角∠COE的度数.
∵四边形ABCD是矩形,
∴AO=CO=BO=OD,(矩形的对角线相等且互相平分)
∵∠AOB=60°,
∴∠COD=60°,(对顶角相等)
∴△AOB和△COD为等边三角形,(有一个角是60°的等腰三角形是等边三角形),
∴∠BAC=60°,CD=OC,
则∠ACB=30°,(直角三角形两锐角互余)
∵DE平分∠ADC,
∴∠EDC=45°,
可得△DCE为等腰直角三角形,
∴CD=EC,
∴EC=OC,(等量代换)
∴∠COE=∠CEO,
∴∠COE=75°(三角形内角和是180°).
故答案为75°.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目