题目内容
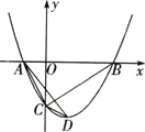
【题目】如图,在平面直角坐标系中,过A(-1,0)、B(3,0)两点的抛物线交y轴于点C,其顶点为点D,设△ACD的面积为S1,△ABC的面积为S2.小芳经探究发现:S1︰S2是一个定值.这个定值为________.
【答案】![]()
【解析】
设二次函数的解析式是y=a(x+1)(x-3),即y=ax-2ax-3a,即可求得C的坐标,表示出的值S2,然后利用待定系数法求得AD的解析式,进而求得EO的值,得到CE的长,根据三角形面积公式即可求得S1,进而求解.
设二次函数的解析式是y=a(x+1)(x3),即y=ax2ax3a,AD与CB交于点E.
令x=0,解得:y=3a,则OC=3a.
∴S2= ![]() ABOC=
ABOC= ![]() ×43a=6a;
×43a=6a;
∵D是抛物线的顶点。
∴D的横坐标是:![]() (1+3)=1,把x=1代入二次函数解析式得:y=4a,则D的坐标是(1,4a).
(1+3)=1,把x=1代入二次函数解析式得:y=4a,则D的坐标是(1,4a).
设直线AD的解析式是y=kx+b.
根据题意得: k+b=0,k+b=4a
解得:k=b=2a
则直线AD的解析式是:y=2ax2a.
在y=2ax2a中,令x=0,解得:y=2a.
则CE=3a2a=a.
∴S1=S△ACE +S△CDE=![]() CE×a+
CE×a+![]() CE×a=a.
CE×a=a.
∴S1: S2=a:6a= ![]()
故答案是:![]()

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目