题目内容
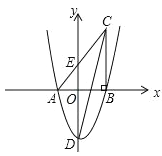
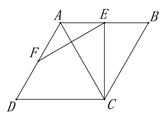
【题目】如图,四边形ABCD是边长为2的菱形,E,F分别是AB,AD的中点,连接EF,EC,将△FAE绕点F旋转180°得到△FDM.
(1)补全图形并证明:EF⊥AC;
(2)若∠B=60°,求△EMC的面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)①按要求画出图形即可;②连接BD,由已知条件可知EF是△ABD的中位线,由此可得EF∥BD,由菱形的性质可得AC⊥BD,从而可得EF⊥AC;
(2)由已知条件易得△ABC是等边三角形,结合点E是AB的中点可得CE⊥AB,结合AB∥CD可得CE⊥MC,在Rt△BCE中由已知条件求得CE的长,由已知易得AE=1,由此可得MD=1,从而可得CD的长,这样即可由S△CME=![]() MC·CE求出其面积了.
MC·CE求出其面积了.
(1)①补全图形如下图所示:
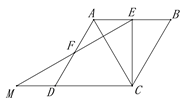
②如下图,连接DB,
∵四边形ABCD是菱形,
∴DB⊥AC,
∵E,F分别是AB,AD的中点,
∴EF∥BD.
∴EF⊥AC.
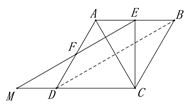
(2)∵四边形ABCD是菱形,
∴AB=BC.
∵∠B=60°,
∴△ABC是等边三角形,
∵E是AB的中点,
∴CE⊥AB,CE⊥MC.
即△EMC是直角三角形,且CE=BC×sin60°=![]() .
.
由(1)得MD=AE=![]() AB=1.
AB=1.
∴MC=MD+DC=3.
∴S△EMC=![]() MC×CE=
MC×CE=![]() .
.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案【题目】为了解我市市区初中生“绿色出行”方式的情况,某初中数学兴趣小组以问卷调查的形式,随机调查了本校部分学生上下学的主要出行方式,并将调查结果绘制了如图所示的两幅不完整的统计图,请根据图中提供的信息解答以下问题:
种类 |
|
|
|
|
|
出行方式 | 步行 | 公交车 | 自行车 | 私家车 | 出租车 |
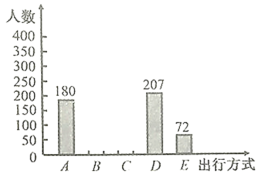
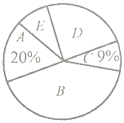
(1)参与本次问卷调查的学生共有_________人,其中选择![]() 类的人数所占的百分比为____________.
类的人数所占的百分比为____________.
(2)请通过计算补全条形统计图,并计算扇形统计图中![]() 类所对应扇形的圆心角的度数.
类所对应扇形的圆心角的度数.
(3)我市市区初中生每天约![]() 人出行,若将
人出行,若将![]() ,
,![]() ,
,![]() 这三类出行方式均视为“绿色出行”方式,请估计我市市区初中生选取“绿色出行”方式的人数.
这三类出行方式均视为“绿色出行”方式,请估计我市市区初中生选取“绿色出行”方式的人数.