ЬтФПФкШн
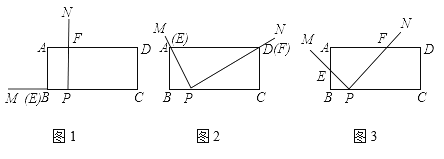
ЁОЬтФПЁПШчЭМ1ЃЌдкОиаЮABCDжаЃЌAB=2ЃЌBC=5ЃЌBP=1ЃЌЁЯMPN=90ЁуЃЌНЋЁЯMPNШЦЕуPДгPBДІПЊЪМЫГЪБеыЗНЯђа§зЊЃЌPMНЛБпABгкЕуEЃЌPNНЛБпADгкЕуFЃЌЕБPEа§зЊжСPAДІЪБЃЌЁЯMPNЕФа§зЊЫцМДЭЃжЙ.
ЃЈ1ЃЉШчЭМ2ЃЌдка§зЊжаЗЂЯжЕБPMОЙ§ЕуAЪБЃЌPNвВОЙ§ЕуDЃЌЧѓжЄЃКЁїABP ЁзЁїPCD
ЃЈ2ЃЉШчЭМ3ЃЌдка§зЊЙ§ГЬжаЃЌ![]() ЕФжЕЪЧЗёЮЊЖЈжЕЃПШєЪЧЃЌЧыЧѓГіИУЖЈжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩ
ЕФжЕЪЧЗёЮЊЖЈжЕЃПШєЪЧЃЌЧыЧѓГіИУЖЈжЕЃЛШєВЛЪЧЃЌЧыЫЕУїРэгЩ
ЃЈ3ЃЉЩшAE![]() ЃЌСЌНсEFЃЌдђдка§зЊЙ§ГЬжаЃЌЕБ
ЃЌСЌНсEFЃЌдђдка§зЊЙ§ГЬжаЃЌЕБ![]() ЮЊКЮжЕЪБЃЌЁїBPEгыЁїPEFЯрЫЦ.
ЮЊКЮжЕЪБЃЌЁїBPEгыЁїPEFЯрЫЦ.
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉ![]() ЕФжЕЪЧЖЈжЕЃЌИУЖЈжЕЮЊ
ЕФжЕЪЧЖЈжЕЃЌИУЖЈжЕЮЊ![]() ЃЛЃЈ3ЃЉЕБ
ЃЛЃЈ3ЃЉЕБ![]() Лђ
Лђ![]() ЪБЃЌЁїBPEгыЁїPEFЯрЫЦ
ЪБЃЌЁїBPEгыЁїPEFЯрЫЦ
ЁОНтЮіЁП
ЃЈ1ЃЉвђЮЊдкОиаЮжаЃЌЫљвджЛвЊдйжЄУїЁЯBAP=ЁЯCPDМДПЩЃЛЃЈ2ЃЉжЄУїБпБШЮЊЖЈжЕЃЌПМТЧЯрЫЦШ§НЧаЮЃЌЙ§ЕуFзїFGЁЭBCгкGЃЌДДдьЁїPGFВЂжЄУїЦфгыЁїEBP ЯрЫЦЃЛЃЈ3ЃЉЪЙЁїBPE ЁзЁїPFEЃЌФЧУД![]() ЃЌЫуГіmжЕЃЌЗДжЄЯрЫЦ.
ЃЌЫуГіmжЕЃЌЗДжЄЯрЫЦ.
ЃЈ1ЃЉжЄУїЃКЁпЫФБпаЮABCDЪЧОиаЮ
ЁрЁЯB=ЁЯC=90Ёу
ЁрЁЯBAP+ЁЯBPA=90Ёу
ЁпЁЯMPN=90Ёу
ЁрЁЯCPD+ЁЯBPA=90Ёу
ЁрЁЯBAP=ЁЯCPD
ЁрЁїABP ЁзЁїPCD
ЃЈ2ЃЉЙ§ЕуFзїFGЁЭBCгкG
ЁрЁЯFGP=90Ёу
ЁрЁЯFGP=ЁЯBЃЌЁЯPFG+ЁЯFPG=90Ёу
взжЊЫФБпаЮABGFЪЧОиаЮЃЌ
ЁрFG=AB=2
ЁпЁЯMPN=90Ёу
ЁрЁЯEPB+ЁЯFPG=90Ёу
ЁрЁЯEPB=ЁЯFPG
ЁрЁїEBP ЁзЁїPGF
Ёр![]()
Ёр![]() ЕФжЕЪЧЖЈжЕЃЌИУЖЈжЕЮЊ
ЕФжЕЪЧЖЈжЕЃЌИУЖЈжЕЮЊ![]()
ЃЈ3ЃЉЁпAE![]()
ЁрBE![]()
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ
ЁпЁЯB=ЁЯEPF=90Ёу
ЁрЁїBPE ЁзЁїPFE
Ёр![]()
Ёр![]()
Ёр![]()
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ
ЁпЁЯB=ЁЯEPF=90Ёу
ЁрЁїBPE ЁзЁїPEF
Ёр![]()
Ёр![]()
Ёр![]()
злЩЯЃЌЕБ![]() Лђ
Лђ![]() ЪБЃЌЁїBPEгыЁїPEFЯрЫЦ.
ЪБЃЌЁїBPEгыЁїPEFЯрЫЦ.

 AМгН№Ьт ЯЕСаД№АИ
AМгН№Ьт ЯЕСаД№АИ ШЋгХВтЪдОэЯЕСаД№АИ
ШЋгХВтЪдОэЯЕСаД№АИ