题目内容
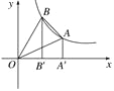
【题目】如图，点A在双曲线y＝
（x＞0）上，点B在双曲线y＝
（x＞0）上，且AB∥x轴，BC∥y轴，点C在x轴上，则△ABC的面积为_____．
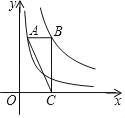
【答案】1.5
【解析】
作AE⊥x轴于E，BF⊥x轴于F，延长BA交y轴于点D，如图，根据反比例函数比例系数k的几何意义得S矩形AEOD＝1，S矩形BFOD＝4，于是得到S矩形AEFB＝3，然后根据矩形的性质和三角形面积公式易得S△ABC＝S△FAB＝1.5．
解：作AE⊥x轴于E，BF⊥x轴于F，延长BA交y轴于点D，如图，
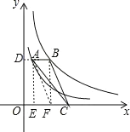
∵AB∥x轴，
∴S矩形AEOD＝1，S矩形BFOD＝4，
∴S矩形AEFB＝41＝3，
∴S△FAB＝1.5，
∴S△ABC＝S△FAB＝1.5．
故答案为1.5．
练习册系列答案
相关题目
