题目内容
【题目】如图,已知点I是△ABC的角平分线的交点.若AB+BI=AC,设∠BAC=α,则∠AIB=______(用含α的式子表示)

【答案】![]()
【解析】
在AC上截取AD=AB,易证△ABI≌△ADI,所以BI=DI,由AB+BI=AC,可得DI=DC,
设∠DCI=β,则∠ADI=∠ABI=2β,然后用三角形内角和可推出β与α的关系,进而求得∠AIB.
解:如图所示,在AC上截取AD=AB,连接DI,
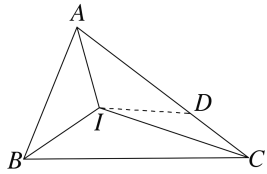
点I是△ABC的角平分线的交点
所以有∠BAI=∠DAI,∠ABI=∠CBI,∠ACI=∠BCI,
在△ABI和△ADI中,
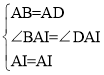
∴△ABI≌△ADI(SAS)
∴DI=BI
又∵AB+BI=AC,AB+DC=AC
∴DI=DC
∴∠DCI=∠DIC
设∠DCI=∠DIC=β
则∠ABI=∠ADI=2∠DCI=2β
在△ABC中,
∠BAC+2∠ABI+2∠DCI=180°,即![]() ,
,
∴![]()
在△ABI中,![]()
![]()
![]()
![]()

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目