题目内容
【题目】如图,已知△ABC,AB、AC的垂直平分线的交点D恰好落在BC边上
(1)判断△ABC的形状
(2)若点A在线段DC的垂直平分线上,求![]() 的值
的值
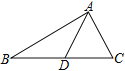
【答案】(1)△ABC为直角三角形;(2)![]()
【解析】
(1)由垂直平分线的性质可得AD=BD,AD=CD,再由等腰三角形底角相等,可推出∠BAC=90°,即△ABC为直角三角形.
(2)A在DC的垂直平分线上,则AD=AC,由(1)可得AD=AC=BD=CD,可得出![]() .
.
解:(1)∵D在AB的垂直平分线上,∴AD=BD,∴∠B=∠BAD
∵D点在AC的垂直平分线上,∴AD=CD,∴∠C=∠CAD
在△ABC中,
∠B+∠C+∠BAD+∠CAD=180°
∴![]() ,即∠BAC=90°
,即∠BAC=90°
∴△ABC为直角三角形.
(2)∵A在DC的垂直平分线上
∴AD=AC
由(1)可得AD=AC=BD=CD
∴![]()

练习册系列答案
相关题目