题目内容
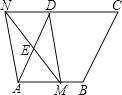
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF.
(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.

【答案】(1)证明过程见解析;(2)等腰直角三角形,证明过程见解析.
【解析】
试题(1)根据在等腰直角△ABC中,∠ACB=90°,AC=BC,利用F是AB中点,∠A=∠FCE=∠ACF=45°,即可证明:△ADF≌△CEF.
(2)利用△ADF≌△CEF,∠AFD+∠DFC=∠CFE+∠DFC,和∠AFC=90°即可证明△DFE是等腰直角三角形.
试题解析:(1)在等腰直角△ABC中,∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
又∵F是AB中点,
∴∠ACF=∠FCB=45°,
即,∠A=∠FCE=∠ACF=45°,且AF=CF,
在△ADF与△CEF中,
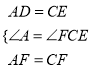 ,
,
∴△ADF≌△CEF;
(2)由(1)可知△ADF≌△CEF,
∴DF=FE,
∴△DFE是等腰三角形,
又∵∠AFD=∠CFE,
∴∠AFD+∠DFC=∠CFE+∠DFC,
∴∠AFC=∠DFE,
∵∠AFC=90°,
∴∠DFE=90°,
∴△DFE是等腰直角三角形.

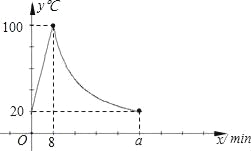
【题目】某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温和时间的关系如下图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的关系式;
(2)求出图中a的值;
(3)下表是该小学的作息时间,若同学们希望在上午第一节下课8:20时能喝到不超过40℃的开水,已知第一节下课前无人接水,请直接写出生活委员应该在什么时间或时间段接通饮水机电源.(不可以用上课时间接通饮水机电源)
时间 | 节次 | |
上 午 | 7:20 | 到校 |
7:45~8:20 | 第一节 | |
8:30~9:05 | 第二节 | |
… | … | |
【题目】20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准偏差 | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐与最轻的一筐相差多少千克?
(2)这20筐白菜的平均质量比标准质量多或少多少千克?
(3)若白菜每千克售价2元,则出售这20筐白菜可卖多少元?
【题目】某电压力锅生产厂家计划每天平均生产n台电压力锅,而实际产量与计划产量相比有出入.下表记录了某周五个工作日每天实际产量情况(超过计划产量记为正、少于计划产量记为负):
星期 | 一 | 二 | 三 | 四 | 五 |
实际生产量/台 | +5 | -2 | -4 | +13 | -3 |
(1)用含n的代数式表示本周前三天生产电压力锅的总台数;
(2)该厂实行每日计件工资制:每生产一台电压力锅可得60元,若超额完成任务,则超过部分每台1另奖10元;少生产一台扣15元.当n=100时,那么该厂工人这一周的工资总额是多少元?
(3)若将上面第(2)问中“实行每日计件工资制”改为“实行每周计件工资制”,其他条件不变,当n=100时,在此方式下这一周工人的工资与按日计件的工资哪一个更多?请说明理由.