题目内容
【题目】如图，在RtΔABC中，∠ACB＝90°，AC=9，BC=12，AD是∠BAC的平分线，若点P，Q分别是AD和AC上的动点，则PC＋PQ的最小值是( )
A.
B.
C.12D.15
【答案】B
【解析】
过点D作DE⊥AB于点E，过点E作EQ⊥AC于点Q，EQ交AD于点P，连接CP，此时PC+PQ=EQ是最小值，根据勾股定理可求出AB的长度，再根据EQ⊥AC、∠ACB=90°即可得出EQ∥BC，进而可得出
，代入数据即可得出EQ的长度，此题得解.
解：如图所示，过点D作DE⊥AB于点E，过点E作EQ⊥AC于点Q，EQ交AD于点P，连接CP，此时PC+PQ=EQ是最小值，
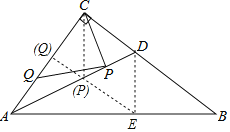
在Rt△ABC中，∠ACB=90°，AC=9，BC=12，
∴
，
∵AD是∠BAC的平分线，
∴∠CAD=∠EAD，
在△ACD和△AED中，
，
∴△ACD≌△AED（AAS），
∴AE=AC=9．
∵EQ⊥AC，∠ACB=90°，
∴EQ∥BC，
，
∴
，
.
故选：B.
练习册系列答案
相关题目
【题目】某商场经营某种品牌的玩具，进价是20元，根据市场调查：在一段时间内，销售单价是30元时，销售量是500件，而销售单价每涨1元，就会少售出10件玩具．
（1）不妨设该种品牌玩具的销售单价为x元（x＞40），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
销售单价（元） | x |
销售量y（件） | __________ |
销售玩具获得利润w（元） | __________ |
（2）在（1）问条件下，若商场获得了8000元销售利润，求该玩具销售单价x应定为多少元．
（3）在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于35元，且商场要完成不少于350件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？
