��Ŀ����
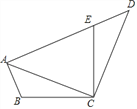
����Ŀ����֪ͼ����һ����Ϊ2a����Ϊ2b�ij����Σ���ͼ���������ü������ȷֳ��ĸ�С�����Σ�Ȼ��ͼ�ҵ���״ƴ��һ�������Σ�
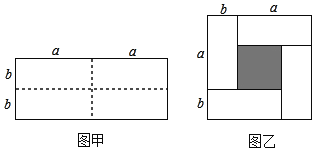
��1���뽫ͼ������Ӱ���������εı߳��ú�a��b�Ĵ���ʽ��ʾ��
��2���������ֲ�ͬ�ķ�����ͼ������Ӱ���ֵ����S��
��3���۲�ͼ�ң�����ϣ�2���еĽ��ۣ�д������������ʽ��![]() ��
��![]() ��ab֮��ĵ�ʽ��
��ab֮��ĵ�ʽ��
��4�����ݣ�3���еĵ�����ϵ������������⣺��![]() ��
��![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
���𰸡�������
��������
��1���۲�ͼ�Ҽ���ȷ�������εı߳���
��2������ͼ�ס�ͼ������Ӱ���ֵ�������ɣ�
��3������ͼ����Ӱ���ֵ�����Ƕ�ֵ�����ɣ�a+b��2����a-b��2��ab֮��ĵ�����ϵʽ��
��4�����ã�3���еĹ�ʽ�õ���a-b��2=��a+b��2-4ab�����ɣ�a-b��2��ֵ��
�⣺��1����ͼ�ҿɵ�С�����εı߳�Ϊa-b��
��2�������٣�S=��a-b��2�������ڣ�S=��a+b��2-4ab��
��3������ͼ����Ӱ���ֵ�����Ƕ�ֵ����a-b��2=��a+b��2-4ab��
��4���ɣ�3���ã���a-b��2=��a+b��2-4ab��
��a+b=8��ab=12��
�ࣨa-b��2=82-4��12=64-48=16��

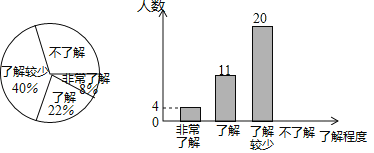
����Ŀ��ij������ѧ��ȤС�����Ժ���y=x2��2|x|��ͼ������ʽ�����̽����̽���������£��벹����������1���Ա���x��ȡֵ��Χ��ȫ��ʵ����x��y�ļ����Ӧֵ�б����£�
x | �� | ��3 | �� | ��2 | ��1 | 0 | 1 | 2 |
| 3 | �� |
y | �� | 3 |
| m | ��1 | 0 | ��1 | 0 |
| 3 | �� |
����m=������
��2�����ݱ������ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㣬�������˺���ͼ���һ���֣��뻭���ú���ͼ�����һ���֣�
��3���۲캯��ͼ��д���������������ʣ�
��4����һ��̽������ͼ���֣�
�ٺ���ͼ����x�������������㣬���Զ�Ӧ�ķ���x2��2|x|=0���� ����ʵ������
�ڷ���x2��2|x|=2��������ʵ����.

�۹���x�ķ���x2��2|x|=a��4��ʵ����ʱ��a��ȡֵ��Χ���� ��