题目内容
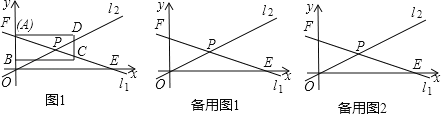
【题目】在平面直角坐标系中,过点A(2,0)的直线![]() 与y轴交于点B,与双曲线
与y轴交于点B,与双曲线![]() 交于点P,点P位于y轴左侧,且到y轴的距离为1,已知tan∠OAB=
交于点P,点P位于y轴左侧,且到y轴的距离为1,已知tan∠OAB=![]() .
.
(1)分别求出直线与双曲线相应的函数表达式;
(2)观察图象,直接写出不等式![]() >
>![]() 的解集.
的解集.

【答案】(1)![]() ;(2)x<-1或0<x<3
;(2)x<-1或0<x<3
【解析】由点A(2,0),可得OA=2,再由tan∠OAB=![]() ,求得OB=1,所以点B的坐标为(0,1),把A、B两点的坐标代入y=kx+b,利用待定系数法求出直线AB的解析式,已知直线上的点P位于y轴左侧,且到y轴的距离为1,即可得点P的横坐标为﹣1,将x=﹣1代入直线AB的解析式求得y的值,即可得点P的坐标,再把点P的坐标代入反比例函数y=
,求得OB=1,所以点B的坐标为(0,1),把A、B两点的坐标代入y=kx+b,利用待定系数法求出直线AB的解析式,已知直线上的点P位于y轴左侧,且到y轴的距离为1,即可得点P的横坐标为﹣1,将x=﹣1代入直线AB的解析式求得y的值,即可得点P的坐标,再把点P的坐标代入反比例函数y=![]() 求得m的值,即可得双曲线相应的函数表达式; (2)再求得直线与双曲线的另一个交点坐标,观察图象即可得
求得m的值,即可得双曲线相应的函数表达式; (2)再求得直线与双曲线的另一个交点坐标,观察图象即可得![]() >
>![]() 的解集.
的解集.
(1)∵点A(2,0),∴OA=2,
∵tan∠OAB=![]() ,∴OB=1,∴点B的坐标为(0,1),
,∴OB=1,∴点B的坐标为(0,1),
直线y=kx+b过点A和点B,所以![]() ,得
,得![]() ,
,
即直线表达式为y=﹣0.5x+1;
∵直线上的点P位于y轴左侧,且到y轴的距离为1.∴点P的横坐标为﹣1,
将x=﹣1代入y=﹣0.5x+1,得y=1.5,∴点P的坐标为(﹣1,1.5),
∵反比例函数y=![]() 的图象经过点P,
的图象经过点P,
∴1.5=![]() ,得m=﹣1.5,
,得m=﹣1.5,
所以双曲线相应的函数表达式为![]()
(2)求得直线与双曲线的另一个交点为(3,0),
观察图象得![]() >
>![]() 的解集为x<-1或0<x<3
的解集为x<-1或0<x<3

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

【题目】股市一周内周六、周日两天不开市,股民小王上周五以每股25.20元的价格买进某公司股票10000股,下表为本周内每天该股票的涨跌情况:
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨 跌情况 | -0.1 | +0.4 | -0.2 | -0.4 | +0.5 |
注:表中正数表示股价比前一天上涨,负数表示股价比前一天下跌.
(1)星期四收盘时,每股多少元?
(2)本周内哪一天股价最高,是多少元?
(3)股民小王本周末将该股票全部售出(不记交易税),小王在本次交易中获利多少元?