题目内容
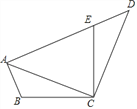
【题目】如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若∠ACB=30°,∠D=45°,求∠AEC的度数.
【答案】(1)证明见解析;(2)75°
【解析】
试题(1)根据同角的余角相等可得到∠ACB=∠DCE,结合条件可得到∠BAC=∠D,再加上BC=CE,可证ΔACB≌ΔDCE,从而求得结论;
(2)由(1)知∠DCE=∠ACB=30°,又∠D=45°,故∠AEC=75°.
试题解析:∵∠BCE=∠ACD=90°,
∴∠ACB+∠ACE=∠ACE+∠DCE,
∴∠ACB=∠DCE,
在△ABC和△DEC中,
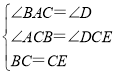 ,
,
∴△ABC≌△DEC(AAS),
∴AC=CD;
(2)∵∠ACD=90°,∠ACB=30°,
∴∠DCE=∠ACB=30°
∵∠D=45°,
∴∠AEC=∠D +∠DCE=45°+30°=75°.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目