题目内容
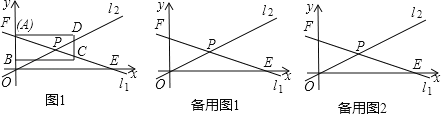
【题目】如图,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,
上,![]()
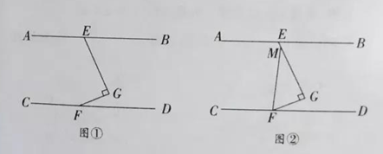
![]() 如图①,若
如图①,若![]() ,判断
,判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 图②,在
图②,在![]() 的结论下,
的结论下,![]() 上有一点
上有一点![]() ,且
,且![]() ,判断
,判断![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)AB∥CD,理由见解析;(2)∠BEG+![]() ∠DFM=90°,理由见解析
∠DFM=90°,理由见解析
【解析】
(1)延长EG交CD于H,根据平角的定义得到∠HGF=∠EGF=90°,根据平行线判定定理即可得到结论;
(2)延长EG交CD于H,根据∠GHF+∠GFH=90°和平行线性质定理即可得到结论;
(1)AB∥CD,
理由:延长EG交CD于H,

∴∠HGF=∠EGF=90°,
∴∠GHF+∠GFH=90°,
∵∠BEG+∠DFG=90°,
∴∠BEG=∠GHF,
∴AB∥CD;
(2)∠BEG+![]() ∠DFM=90°,
∠DFM=90°,
理由:延长EG交CD于H,

∵AB∥CD,
∴∠BEG=∠GHF,
∵EG⊥FG,
∴∠GHF+∠GFH=90°,
∵∠MFG=3∠DFG,
∴∠BEG+![]() ∠DFM =90°;
∠DFM =90°;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如下数据:
轿车行驶的路程 s(km) | 0 | 10 | 20 | 30 | 40 | … |
油箱剩余油量 w(L) | 50 | 49.2 | 48.4 | 47.6 | 46.8 | … |
(1)该轿车油箱的容量为 L,行驶 120km 时,油箱剩余油量为 L;
(2)根据上表的数据,写出油箱剩余油量 w(L)与轿车行驶的路程 s(km)之间的表达式 ;
(3)某人将油箱加满后,驾驶该轿车从 A 地前往 B 地,到达 B 地时邮箱剩余油量为 22L,求 A,B 两地之间的距离.