题目内容
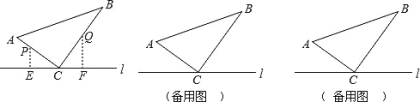
【题目】如图,![]() ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
(1)如图,当 x 2 时,设点 P 运动时间为 ts ,当点 P 在 AC 上,点 Q 在 BC 上时:
①用含 t 的式子表示 CP 和 CQ,则 CP= cm,CQ= cm;
②当 t 2 时,![]() PEC 与
PEC 与![]() QFC 全等吗?并说明理由;
QFC 全等吗?并说明理由;
(2)请问:当 x 3 时,![]() PEC 与
PEC 与![]() QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
【答案】(1)6-t,8-2t;②△PEC≌△CFQ,理由见详解;(2)当 x 3 时,△PEC≌△CFQ,时间可以为:![]() s,
s,![]() ;
;
【解析】
(1)①根据路程=速度×时间,即可解答;
②由运动的时间t=2,得到CP=CQ,然后由垂直定义和余角的性质,得到∠PEC=∠QFC=90°,∠PCE=∠CQF,根据AAS即可得到全等;
(2)根据题意,由△PEC与△QFC全等,得到PC=QC.即可分为三种情况进行①当P在AC上,Q在BC上时,先求出CQ=8-3t,可得6-t=8-3t;②当点P与点Q重合,6-t=3t-8;③当点P在BC上,点Q到点A时,此时有t-6=6;即可解答;
解:(1)①根据题意,当 x 2 时,运动时间为t 秒时,
有AP=t,BQ=2t,
∴CP=6-t,CQ=8-2t,
故答案为:6-t,8-2t;
②当 t 2 时,△PEC≌△CFQ;
理由如下:
当 t 2 时,![]()
∴![]() ,
,
∵∠ACB=90°,
∴∠PCE+∠QCF=90°,
∵PE⊥ l 于 E,QF⊥ l 于 F,
∴∠PEC=∠QFC=90°,
∴∠QCF+∠CQF=90°,
∴∠PCE=∠CQF,
在△PEC和△CFQ中,
有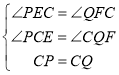 ,
,
∴△PEC≌△CFQ(AAS);
(2)①当P在AC上,Q在BC上时,有![]() ,
,
∵△PEC≌△CFQ,
∴CP=CQ,
即:![]() ,
,
解得:![]() ,
,
②当点P与点Q重合,如图2所示: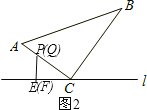
∴△PEC与△QFC全等,
∴6-t=3t-8.
解得:t=3.5.
③当点P在BC上,点Q到点A时,
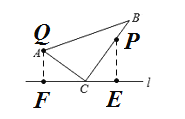
此时:![]()
∴t-6=6,
∴t=12,
即:满足条件的时间为:1秒或3.5秒或12秒.
∴当 x 3 时,时间![]() s,
s,![]() ,有△PEC≌△CFQ;
,有△PEC≌△CFQ;