题目内容
【题目】某校为了了解了解节能减排、垃圾分类等知识的普及情况,从该校2000名学生中随机抽取了部分学生进行调查调查,调查结果分为“非常了解“、“了解”、“了解较少”、“不了解”四类,并将调查结果绘制出以下两幅不完整的统计图,请根据统计图回答下列问题:
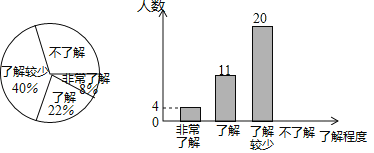
(1)本次调查的学生共有 人,估计该校2000名学生中“不了解”的人数约有 人.
(2)“非常了解”的4人中有A1,A2两名男生,B1,B2两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图和列表的方法,求恰好抽到2名男生的概率.
【答案】(1)50,600;(2)P(恰好抽到2名男生)=![]() .
.
【解析】(1)由“非常了解”的人数及其所占百分比求得总人数,继而由各了解程度的人数之和等于总人数求得“不了解”的人数,用总人数乘以样本中“不了解”人数所占比例可得;
(2)分别用树状图和列表两种方法表示出所有等可能结果,从中找到恰好抽到2名男生的结果数,利用概率公式计算可得.
(1)本次调查的学生总人数为4÷8%=50人,
则不了解的学生人数为50﹣(4+11+20)=15人,
∴估计该校2000名学生中“不了解”的人数约有2000×![]() =600人,
=600人,
故答案为:50、600;
(2)画树状图如下:
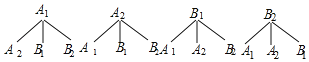
共有12种可能的结果,恰好抽到2名男生的结果有2个,
∴P(恰好抽到2名男生)=![]() .
.
列表如下:
A1 | A2 | B1 | B2 | |
A1 | (A2,A1) | (B1,A1) | (B2,A1) | |
A2 | (A1,A2) | (B1,A2) | (B2,A2) | |
B1 | (A1,B1) | (A2,B1) | (B2,B1) | |
B2 | (A1,B2) | (A2,B2) | (B1,B2) |
由表可知共有12种可能的结果,恰好抽到2名男生的结果有2个,
∴P(恰好抽到2名男生)=![]() .
.

【题目】为了解某品牌轿车的耗油情况,将油箱加满后进行了耗油试验,得到如下数据:
轿车行驶的路程 s(km) | 0 | 10 | 20 | 30 | 40 | … |
油箱剩余油量 w(L) | 50 | 49.2 | 48.4 | 47.6 | 46.8 | … |
(1)该轿车油箱的容量为 L,行驶 120km 时,油箱剩余油量为 L;
(2)根据上表的数据,写出油箱剩余油量 w(L)与轿车行驶的路程 s(km)之间的表达式 ;
(3)某人将油箱加满后,驾驶该轿车从 A 地前往 B 地,到达 B 地时邮箱剩余油量为 22L,求 A,B 两地之间的距离.