题目内容
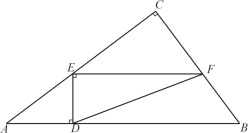
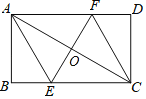
【题目】如图,过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF,若AB=2![]() ,∠DCF=30°,则EF的长为( )
,∠DCF=30°,则EF的长为( )

A. 4B. 6C. ![]() D. 2
D. 2![]()
【答案】A
【解析】
求出∠ACB=∠DAC,然后利用“角角边”证明△AOF和△COE全等,根据全等三角形对应边相等可得OE=OF,再根据对角线互相垂直平分的四边形是菱形得到四边形AECF是菱形,再求出∠ECF=60°,然后判断出△CEF是等边三角形,根据等边三角形的三条边都相等可得EF=CF,根据矩形的对边相等可得CD=AB,然后求出CF,从而得解.
∵矩形对边AD∥BC,
∴∠ACB=∠DAC,
∵O是AC的中点,
∴AO=CO,
在△AOF和△COE中,
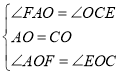 ,
,
∴△AOF≌△COE(ASA),
∴OE=OF,
又∵EF⊥AC,
∴四边形AECF是菱形,
∵∠DCF=30°,
∴∠ECF=90°﹣30°=60°,
∴△CEF是等边三角形,
∴EF=CF,
∵AB=2![]() ,
,
∴CD=AB=2![]() ,
,
∵∠DCF=30°,
∴CF=![]() =2
=2![]() ÷
÷![]() =4,
=4,
∴EF=4,
故选A.

 阅读快车系列答案
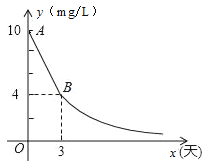
阅读快车系列答案【题目】环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0 mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,其中第3天时硫化物的浓度降为4 mg/L.从第3天起所排污水中硫化物的浓度y与时间x满足下面表格中的关系:
时间x(天) | 3 | 4 | 5 | 6 | 8 | …… |
硫化物的浓y(mg/L) | 4 | 3 | 2.4 | 2 | 1.5 |
(1)求整改过程中当0≤x<3时,硫化物的浓度y与时间x的函数表达式;
(2)求整改过程中当x≥3时,硫化物的浓度y与时间x的函数表达式;
(3)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0 mg/L?为什么?