Question

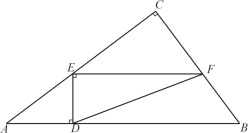
【题目】如图，在Rt△ABC中，∠C＝90°，AC＝8，BC＝6，D为AB边上的动点，过点D作DE⊥AB交边AC于点E，过点E作EF⊥DE交BC于点F，连接DF．

（1）当AD＝4时，求EF的长度；

（2）求△DEF的面积的最大值；

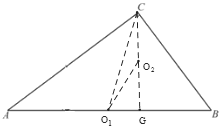
（3）设O为DF的中点，随着点D的运动，则点O的运动路径的长度为______．

Answer 1

【答案】（1），（2）6，（3）

【解析】

（1）利用勾股定理可求出AB的长，根据∠A＝∠A，∠EDA＝∠C＝90°可证明△AED∽△ABC，即可求出AE、CE的长，由∠EDA＝∠DEF＝90°可得EF//AB，即可证明△CEF∽△ACB，根据相似三角形的性质即可求出EF的长；（2）设AD＝x.由△AED∽△ABC可得＝＝，即可用x表示出DE、AE的长，进而可表示CE的长，由△CEF∽△ACB可得＝，即可用x表示出EF的长，进而可用x表示出△DEF的面积，根据二次函数的性质即可求出△DEF的面积的最大值；（3）过C作CG⊥AB于G，当点D与A点重合时，点O为AB中点，当点D与点G重合时，点O为CG的中点，当点D在点G右边时，DE与AC无交点，点O不存在，设AB中点为O1，CG的中点为O2，根据△ABC的面积可求出CG的长，即可得O2G的长，利用勾股定理可求出BG的长，即可得O1G的长，利用勾股定理求出O1O2的长即可.

（1）∵在Rt△ABC中，∠C＝90°，

∴AB＝＝＝10．

∵DE⊥AB，

∴∠EDA＝90°．

∵∠A＝∠A，∠EDA＝∠C＝90°，

∴△AED∽△ABC，

∴＝．

∴AE＝AB＝5．

∴CE＝AC－AE＝8－5＝3．

∵DE⊥AB，

∴∠DEF＝90°．

∵∠EDA＝∠DEF＝90°，

∴EF∥AB．

∴△CEF∽△ACB，

∴＝．

∴EF＝·AB＝．

（2）解：设AD＝x.

∵△AED∽△ABC，

∴＝＝．

∴DE＝·BC＝x，AE＝·AB＝x．

∴CE＝AC－AE＝8－x．

∵△CEF∽△ACB，

∴＝．

∴EF＝·AB＝10－x．

∴S△DEF＝DE·EF＝－x2＋x＝－(x－)2＋6．

∴当x＝时，S△DEF取最大值为6．

因此，△DEF的面积的最大值为6．

（3）过C作CG⊥AB于G，

当点D与A点重合时，点O为AB中点，当点D与点G重合时，点O为CG的中点，当点D在点G右边时，DE与AC无交点，点O不存在，设AB中点为O1，CG的中点为O2，

∴O1O2为点O的运动路径的长度，

∵S△ABC=ACBC=ABCG，

∴CG===，

∴O2G=CG=，BG==，

∵AB=10，

∴O1B=5，

∴O1G= O1B-BG=，

∴O1O2===.