МвДҝДЪИЭ
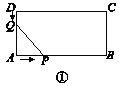
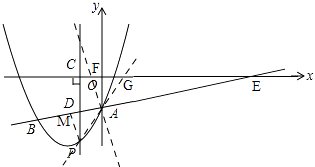
ЎҫМвДҝЎҝИзНјЈ¬ЕЧОпПЯy=x2+bx+cУлЦұПЯy= ![]() x©Ғ3Ҫ»УЪAЎўBБҪөгЈ¬ЖдЦРөгAФЪyЦбЙПЈ¬өгBЧшұкОӘЈЁ©Ғ4Ј¬©Ғ5Ј©Ј¬өгPОӘyЦбЧуІаөДЕЧОпПЯЙПТ»¶ҜөгЈ¬№эөгPЧчPCЎНxЦбУЪөгCЈ¬Ҫ»ABУЪөгDЈ®
x©Ғ3Ҫ»УЪAЎўBБҪөгЈ¬ЖдЦРөгAФЪyЦбЙПЈ¬өгBЧшұкОӘЈЁ©Ғ4Ј¬©Ғ5Ј©Ј¬өгPОӘyЦбЧуІаөДЕЧОпПЯЙПТ»¶ҜөгЈ¬№эөгPЧчPCЎНxЦбУЪөгCЈ¬Ҫ»ABУЪөгDЈ®
ЈЁ1Ј©ЗуЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ2Ј©ТФOЈ¬AЈ¬PЈ¬DОӘ¶ҘөгөДЖҪРРЛДұЯРОКЗ·сҙжФЪЈҝИзҙжФЪЈ¬ЗуөгPөДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЛөГчАнУЙЈ®
ЈЁ3Ј©өұөгPФЛ¶ҜөҪЦұПЯABПВ·ҪДіТ»ҙҰКұЈ¬№эөгPЧчPMЎНABЈ¬ҙ№ЧгОӘMЈ¬Б¬ҪУPAК№ЎчPAMОӘөИСьЦұҪЗИэҪЗРОЈ¬ЗлЦұҪУРҙіцҙЛКұөгPөДЧшұкЈ®
Ўҫҙр°ёЎҝ
ЈЁ1Ј©
ҪвЈәЎЯЦұПЯy= ![]() x©Ғ3Ҫ»УЪAЎўBБҪөгЈ¬ЖдЦРөгAФЪyЦбЙПЈ¬
x©Ғ3Ҫ»УЪAЎўBБҪөгЈ¬ЖдЦРөгAФЪyЦбЙПЈ¬
ЎаAЈЁ0Ј¬©Ғ3Ј©Ј¬
ЎЯBЈЁ©Ғ4Ј¬©Ғ5Ј©Ј¬
Ўа ![]() Ј¬
Ј¬
Ўа 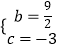 Ј¬
Ј¬
ЎаЕЧОпПЯҪвОцКҪОӘy=x2+ ![]() x©Ғ3
x©Ғ3
ЈЁ2Ј©
ҪвЈәҙжФЪЈ¬
ЙиPЈЁmЈ¬m2+ ![]() m©Ғ3Ј©Ј¬ЈЁmЈј0Ј©Ј¬
m©Ғ3Ј©Ј¬ЈЁmЈј0Ј©Ј¬
ЎаDЈЁmЈ¬ ![]() m©Ғ3Ј©Ј¬
m©Ғ3Ј©Ј¬
ЎаPD=|m2+4m|
ЎЯPDЎОAOЈ¬
ЎаөұPD=OA=3Ј¬№КҙжФЪТФOЈ¬AЈ¬PЈ¬DОӘ¶ҘөгөДЖҪРРЛДұЯРОЈ¬
Ўа|m2+4m|=3Ј¬
ўЩ өұm2+4m=3КұЈ¬
Ўаm1=©Ғ2©Ғ ![]() Ј¬m2=©Ғ2+
Ј¬m2=©Ғ2+ ![]() ЈЁЙбЈ©Ј¬
ЈЁЙбЈ©Ј¬
Ўаm2+ ![]() m©Ғ3=©Ғ1©Ғ
m©Ғ3=©Ғ1©Ғ ![]() Ј¬
Ј¬
ЎаPЈЁ©Ғ2©Ғ ![]() Ј¬©Ғ1©Ғ
Ј¬©Ғ1©Ғ ![]() Ј©Ј¬
Ј©Ј¬
ўЪөұm2+4m=©Ғ3КұЈ¬
Ўаm1=©Ғ1Ј¬m2=©Ғ3Ј¬
ўсЎўm1=©Ғ1Ј¬
Ўаm2+ ![]() m©Ғ3=©Ғ
m©Ғ3=©Ғ ![]() Ј¬
Ј¬
ЎаPЈЁ©Ғ1Ј¬©Ғ ![]() Ј©Ј¬
Ј©Ј¬
ўтЎўm2=©Ғ3Ј¬
Ўаm2+ ![]() m©Ғ3=©Ғ
m©Ғ3=©Ғ ![]() Ј¬
Ј¬
ЎаPЈЁ©Ғ3Ј¬©Ғ ![]() Ј©Ј¬
Ј©Ј¬
ЎаөгPөДЧшұкОӘЈЁ©Ғ2©Ғ ![]() Ј¬©Ғ1©Ғ
Ј¬©Ғ1©Ғ ![]() Ј©Ј¬ЈЁ©Ғ1Ј¬©Ғ
Ј©Ј¬ЈЁ©Ғ1Ј¬©Ғ ![]() Ј©Ј¬ЈЁ©Ғ3Ј¬©Ғ
Ј©Ј¬ЈЁ©Ғ3Ј¬©Ғ ![]() Ј©
Ј©
ЈЁ3Ј©
ҪвЈә·Ҫ·ЁТ»Ј¬ИзНјЈ¬
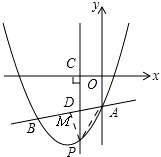
ЎЯЎчPAMОӘөИСьЦұҪЗИэҪЗРОЈ¬
ЎаЎПBAP=45ЎгЈ¬
ЎЯЦұПЯAPҝЙТФҝҙЧцКЗЦұПЯABИЖөгAДжКұХлРэЧӘ45ЎгЛщөГЈ¬
ЙиЦұПЯAPҪвОцКҪОӘy=kx©Ғ3Ј¬
ЎЯЦұПЯABҪвОцКҪОӘy= ![]() x©Ғ3Ј¬
x©Ғ3Ј¬
Ўаk= ![]() =3Ј¬
=3Ј¬
ЎаЦұПЯAPҪвОцКҪОӘy=3x©Ғ3Ј¬
БӘБў  Ј¬
Ј¬
Ўаx1=0ЈЁЙбЈ©x2=©Ғ ![]()
өұx=©Ғ ![]() КұЈ¬y=©Ғ
КұЈ¬y=©Ғ ![]() Ј¬
Ј¬
ЎаPЈЁ©Ғ ![]() Ј¬©Ғ
Ј¬©Ғ ![]() Ј©Ј®
Ј©Ј®
·Ҫ·Ё¶юЈәИзНјЈ¬
ЎЯЦұПЯABҪвОцКҪОӘy= ![]() x©Ғ3Ј¬
x©Ғ3Ј¬
ЎаЦұПЯABУлxЦбөДҪ»өгЧшұкОӘEЈЁ6Ј¬0Ј©Ј¬
№эөгAЧчAFЎНABҪ»xЦбУЪөгFЈ¬
ЎЯAЈЁ0Ј¬©Ғ3Ј©Ј¬
ЎаЦұПЯAFҪвОцКҪОӘy=©Ғ2x©Ғ3Ј¬
ЎаЦұПЯAFУлxЦбөДҪ»өгОӘFЈЁ©Ғ ![]() Ј¬0Ј©Ј¬
Ј¬0Ј©Ј¬
ЎаAE=3 ![]() Ј¬AF=
Ј¬AF= ![]() Ј¬
Ј¬
№эөгAЧчЎПEAFөДҪЗЖҪ·ЦПЯҪ»xЦбУЪөгGЈ¬УлЕЧОпПЯПаҪПУЪөгPЈ¬№эөгPЧчPMЎНABЈ¬
ЎаЎПEAG=45ЎгЈ¬
ЎаЎПBAP=45ЎгЈ¬
јҙЈәЎчPAMОӘөИСьЦұҪЗИэҪЗРОЈ®
ЙиөгGЈЁmЈ¬0Ј©Ј¬
ЎаEG=6©ҒmЈ®FG=m+ ![]() Ј¬
Ј¬
ёщҫЭҪЗЖҪ·ЦПЯ¶ЁАнөГЈ¬ ![]() Ј¬
Ј¬
Ўа ![]() Ј¬
Ј¬
Ўаm=1Ј¬
ЎаGЈЁ1Ј¬0Ј©Ј¬
ЎаЦұПЯAGҪвОцКҪОӘy=3x©Ғ3ўЩЈ¬
ЎЯЕЧОпПЯҪвОцКҪОӘy=x2+ ![]() x©Ғ3ўЪЈ¬
x©Ғ3ўЪЈ¬
БӘБўўЩўЪөГЈ¬x=0ЈЁЙбЈ©»тx=©Ғ ![]() Ј¬
Ј¬
Ўаy=©Ғ ![]() Ј¬
Ј¬
ЎаPЈЁ©Ғ ![]() Ј¬©Ғ
Ј¬©Ғ ![]() Ј©
Ј©
ЎҫҪвОцЎҝЈЁ1Ј©ПИИ·¶ЁіцөгAЧшұкЈ¬И»әуУГҙэ¶ЁПөКэ·ЁЗуЕЧОпПЯҪвОцКҪЈ»ЈЁ2Ј©ПИИ·¶ЁіцPD=|m2+4m|Ј¬өұPD=OA=3Ј¬№КҙжФЪТФOЈ¬AЈ¬PЈ¬DОӘ¶ҘөгөДЖҪРРЛДұЯРОЈ¬өГөҪ|m2+4m|=3Ј¬·ЦБҪЦЦЗйҝцҪшРРМЦВЫјЖЛгјҙҝЙЈ»ЈЁ3Ј©УЙЎчPAMОӘөИСьЦұҪЗИэҪЗРОЈ¬өГөҪЎПBAP=45ЎгЈ¬ҙУ¶шЗуіцЦұПЯAPөДҪвОцКҪЈ¬ЧоәуЗуіцЦұПЯAPәНЕЧОпПЯөДҪ»өгЧшұкјҙҝЙЈ®

ЎҫМвДҝЎҝИзНјКЗЙъ»оЦРіЈјыөДФВАъөДКҫТвНјЈ¬ЗлҪбәПНјКҫ»ШҙрПВБРОКМвЈ®
Т» | ¶ю | Иэ | ЛД | Ое | Бщ | ИХ |
1 | 2 | 3 | 4 | 5 | ||
6 | 7 | 8 | 9 | 10 | 11 | 12 |
13 | 14 | 15 | 16 | 17 | 18 | 19 |
20 | 21 | 22 | 23 | 24 | 25 | 26 |
27 | 28 | 29 | 30 |
(1)ИзНјКЗБнТ»ёцФВөДФВАъЈ¬aұнКҫёГФВЦРДіТ»МмЈ¬bЈ¬cЈ¬dКЗёГФВЦРЖдЛы3МмЈ¬bЈ¬cЈ¬d·ЦұрУлaөД№ШПөЈәbЈҪ________Ј»cЈҪ________Ј»dЈҪ________(УГә¬aөДҙъКэКҪМоҝХ)Ј®
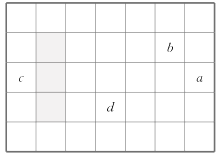
(2)УГТ»ёціӨ·ҪРОҝтИҰіцФВАъЦРөДИэёцКэ(Из НјЦРөДТхУ°)Ј¬ИфХвИэёцКэЦ®әНөИУЪ51Ј¬ФтХвИэёцКэ·ЦұрКЗ¶аЙЩЈҝ
(3)ХвСщИҰіцөДИэёцКэөДәНҝЙДЬКЗ64ВрЈҝОӘКІГҙЈҝ