��Ŀ����
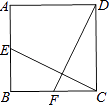
����Ŀ����ͼ�����ڳ�����ABCD����AB��12 cm��BC��6 cm.��P��AB�ߴӵ�A��ʼ���B��2 cm/s���ٶ��ƶ�����Q��DA�ߴӵ�D��ʼ���A��1 cm/s���ٶ��ƶ���
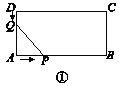
���P��Qͬʱ��������t(s)��ʾ�ƶ���ʱ�䣮
�����֣� DQ��________cm��AP��________cm.(�ú�t�Ĵ���ʽ��ʾ)
����չ��(1)��ͼ������t��________sʱ���߶�AQ���߶�AP��ȣ�
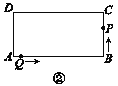
(2)��ͼ������P��Q�ֱ�B��A������˶�����P�����C��ֹͣ�˶���
��tΪ��ֵʱ��AQ��![]() CP?
CP?
��̽��������P��Q�ֱ��B��A���������A��B��C��D��A�ķ����˶�������P���Q��һ������ʱ����ֱ��д���������λ�ã�
���𰸡�t 2t 2
��������
�����֡�������·��=�ٶ���ʱ��,�ɵ�DQ��AP�ij���;
����չ����1����t��ʱ,DQ=tAQ6-t,AP=2t,��6-t=2t�������������⼴��;
(2)��Q��AB����ʱ��AQ��(t��6)cm��CP��(18��2t)cm��,��AQ�ij������߶�CP�ij���һ�뽨�����������⼴��;
��̽��������t����һ������������������з���2t-t=30�����ʱ��t������ʱ�����������λ��.
�����֡� t��2t��
����չ��(1)2��
(2)���������� AQ��(t��6)cm��CP��(18��2t)cm��
����t��6��![]() (18��2t)�����t��7.5.
(18��2t)�����t��7.5.
����t��7.5 sʱ��AQ��![]() CP.
CP.
��̽�������߶�CD���е㴦��