题目内容
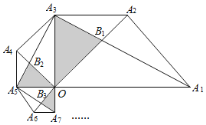
【题目】如图,面积为1的等腰直角△OA1A2,∠OA2A1=90°,且OA2为斜边在△OA1A2外作等腰直角△OA2A3,以OA3为斜边在△OA2A3外作等腰直角△OA3A4,以OA4为斜边在△OA3A4外作等腰直角△OA4A5,…连接A1A3,A3A5,A5A7,…分别与OA2,OA4,OA6,…交于点B1,B2,B3,…按此规律继续下去,记△OB1A3的面积为S1,△OB2A5的面积为S2,△OB3A7的面积为S3,…△OBnA2n+1的面积为Sn,则Sn=__(用含正整数n的式子表示).
【答案】![]()
【解析】
先根据等腰直角三角形的定义求出∠A1OA3=∠OA3A2=90°,得A2A3∥OA1,根据同底等高的两个三角形的面积相等得:![]() ,所以
,所以![]() ,同理得:A4A5∥A3O,同理得:
,同理得:A4A5∥A3O,同理得:![]() ,根据已知的
,根据已知的![]() 1,求对应的直角边和斜边的长:OA2=A1A2
1,求对应的直角边和斜边的长:OA2=A1A2![]() ,A2A3=OA3=1,OA1=2,并利用平行相似证明△A2B1A3∽△OB1A1,列比例式可以求A2B1
,A2A3=OA3=1,OA1=2,并利用平行相似证明△A2B1A3∽△OB1A1,列比例式可以求A2B1![]() ,根据面积公式计算S1
,根据面积公式计算S1![]() ,同理得:S2
,同理得:S2![]() ,从而得出规律.
,从而得出规律.
∵△OA1A2、△OA2A3是等腰直角三角形,∴∠A1OA2=∠A2OA3=45°,∴∠A1OA3=∠OA3A2=90°,∴A2A3∥OA1,∴![]() (同底等高),∴
(同底等高),∴![]() ,∴
,∴![]() ,
,
同理得:A4A5∥A3O,
![]() ,
,
∵![]() 1,∴
1,∴![]() OA2A1A2=1.
OA2A1A2=1.
∵OA2=A1A2,∴OA2=A1A2![]() ,∴A2A3=OA3=1,OA1=2.
,∴A2A3=OA3=1,OA1=2.
∵A2A3∥OA1,∴△A2B1A3∽△OB1A1,∴![]() ,
,
∵A2O![]() ,∴A2B1
,∴A2B1![]() ,∴S1
,∴S1![]() A1A2A2B1
A1A2A2B1![]() ,
,
同理得:OA4=A3A4![]() ,A4A5
,A4A5![]() ,∴△A4A5B2∽△OA3B2,∴
,∴△A4A5B2∽△OA3B2,∴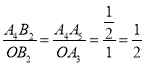 ,∴A4B2
,∴A4B2![]() ,∴S2
,∴S2![]() ,
,
所以得出规律:Sn![]() Sn﹣1
Sn﹣1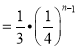 .
.
故答案为: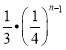 .
.

练习册系列答案
相关题目