题目内容
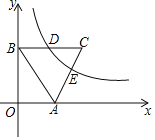
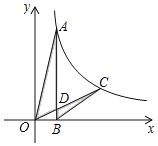
【题目】如图,已知点A,点C在反比例函数y=![]() (k>0,x>0)的图象上,AB⊥x轴于点B,OC交AB于点D,若CD=OD,则△AOD与△BCD的面积比为__.
(k>0,x>0)的图象上,AB⊥x轴于点B,OC交AB于点D,若CD=OD,则△AOD与△BCD的面积比为__.
【答案】3.
【解析】
作CE⊥x轴于E,如图,利用平行线分线段成比例得到![]() =
=![]() =
=![]() =
=![]() ,设D(m,n),则C(2m,2n),再根据反比例函数图象上点的坐标特征得到k=4mn,则A(m,4n),然后根据三角形面积公式用m、n表示S△AOD和S△BCD,从而得到它们的比.
,设D(m,n),则C(2m,2n),再根据反比例函数图象上点的坐标特征得到k=4mn,则A(m,4n),然后根据三角形面积公式用m、n表示S△AOD和S△BCD,从而得到它们的比.
作CE⊥x轴于E,如图,

∵DB∥CE,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
设D(m,n),则C(2m,2n),
∵C(2m,2n)在反比例函数图象上,
∴k=2m×2n=4mn,
∴A(m,4n),
∵S△AOD=![]() ×(4n﹣n)×m=
×(4n﹣n)×m=![]() mn,S△BCD=
mn,S△BCD=![]() ×(2m﹣m)×n=
×(2m﹣m)×n=![]() mn
mn
∴△AOD与△BCD的面积比=![]() mn:
mn:![]() mn=3.
mn=3.
故答案为3.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目