题目内容
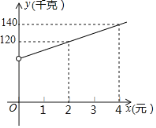
【题目】铁岭市某商贸公司以每千克40元的价格购进一种干果，计划以每千克60元的价格销售，为了让顾客得到更大的实惠，现决定降价销售，已知这种干果销售量y(千克)与每千克降价x(元)(0＜x＜20)之间满足一次函数关系，其图象如图所示：
(1)求y与x之间的函数关系式；
(2)商贸公司要想获利2090元，则这种干果每千克应降价多少元？
(3)该干果每千克降价多少元时，商贸公司获利最大？最大利润是多少元？
【答案】(1)y＝10x+100；(2)这种干果每千克应降价9元；(3)该干果每千克降价5元时，商贸公司获利最大，最大利润是2250元．
【解析】
（1）由待定系数法即可得到函数的解析式；
（2）根据销售量×每千克利润＝总利润列出方程求解即可；
（3）根据销售量×每千克利润＝总利润列出函数解析式求解即可．
(1)设y与x之间的函数关系式为：y＝kx+b，
把(2，120)和(4，140)代入得，
，
解得：
，
∴y与x之间的函数关系式为：y＝10x+100；
(2)根据题意得，(60﹣40﹣x)(10x+100)＝2090，
解得：x＝1或x＝9，
∵为了让顾客得到更大的实惠，
∴x＝9，
答：这种干果每千克应降价9元；
(3)该干果每千克降价x元，商贸公司获得利润是w元，
根据题意得，w＝(60﹣40﹣x)(10x+100)＝﹣10x2+100x+2000，
∴w＝﹣10(x﹣5)2+2250，
∵a=-10
，∴当x＝5时，
故该干果每千克降价5元时，商贸公司获利最大，最大利润是2250元．
练习册系列答案
相关题目
