Question

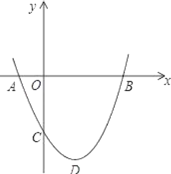
【题目】如图，二次函数y＝ax2+bx+c（a＞0）图象的顶点为点D，其图象与x轴的交点A，B的横坐标分别为﹣1和3，给出下列结论：①2a﹣b＝0；②a+b+c＜0；③3a+c＝0；④当a＝时，△ABD是等腰直角三角形．其中，正确的结论有（ ）

A.①②③B.③④C.②③④D.②④

Answer 1

【答案】C

【解析】

根据二次函数的对称轴、二次函数图像上点的特征、勾股定理及其逆定理分析解答即可．

解：其图象与x轴的交点A，B的横坐标分别为﹣1和3，则函数的对称轴为直线x＝1，

①∵x＝1＝﹣，∴b＝﹣2a，故不符合题意；

②由图象知，当x＝1时，y＝a+b+c＜0，符合题意；

③当x＝﹣1时，y＝a﹣b+c＝0，∵b＝﹣2a，∴3a+c＝0，符合题意；

④函数的表达式为：y＝(x+1)(x﹣3)= (x-1)2-2，则点A、B、D的坐标分别为：(﹣1，0)、(3，0)、(1，﹣2)，AB2＝16，AD2＝4+4＝8，BD2＝8，故△ABD是等腰直角三角形符合题意；

故选：C．