题目内容
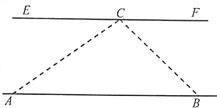
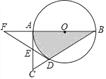
【题目】如图,在Rt△ABC中,∠BAC=90°,以AB为直径作⊙O交BC于点D,E为AC的中点,连接DE并延长交BA的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若∠F=30°,⊙O的半径为2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1) 连接OD、AD,利用直径所对圆周角是直角,可求得△ADC是直角三角形,利用半径构成的等腰三角形找等角,可得∠ODE=90°.(2)求出直角三角形和扇形的面积求和.
试题解析:
解:(1)如图,连接OD、AD,
∵AB为⊙O的直径,
∴△ADC是直角三角形,
∵E为AC的中点,
∴AE=EC=DE,
∴∠ADE=∠DAE,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠BAC=90°,
∴∠OAD+∠DAE=90°,
∴∠ODA+∠ADE=90°,
即∠ODE=90°,OD⊥DE,
∴DE是⊙O的切线;
(2)∵∠F=30° OD⊥DE,
∴∠AOD=60°
又∵r=2![]() .
.
∴图中阴影部分面积=![]() AD
AD![]() =
=![]() .
.

练习册系列答案
相关题目
【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(度) | 电费价格(元/度) |
| 0.48 |
| 0.53 |
| 0.78 |
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,则李叔家七月份最多可用电的度数是( ).
A. 100B. 400C. 396D. 397