题目内容
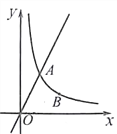
【题目】如图，抛物线y=ax2+bx(a≠0)的图象过原点O和点A(1， 
)，且与x轴交于点B，△AOB的面积为
。
(1)求抛物线的解析式；
(2)若抛物线的对称轴上存在一点M，使△AOM的周长最小，求M点的坐标；
(3)点F是x轴上一动点，过F作x轴的垂线，交直线AB于点E，交抛物线于点P，且PE=
，直接写出点E的坐标(写出符合条件的两个点即可)。
【答案】（1）
；（2）M（
， 
）；（3）（下列四个中任意两个正确）（0， 
）（
， 
）（
， 
）（
， 
）
【解析】试题分析：（1）由△AOB的面积得到OB的长，进而得出点B的坐标．再把A、B的坐标代入抛物线的解析式，解方程组即可得出结论；
（2）先求出抛物线的对称轴，由点B与点O关于对称轴对称，得到直线AB与对称轴的交点就是所要求的点M．由直线AB过A、B两点，得到直线AB的解析式，再求出直线AB和对称轴的交点即可；
（3）设F（x，0），表示出E，P的坐标，进而得到PE的长，解方程即可得出结论．
试题解析：解：（1）∵△AOB的面积为
， 点A（1， 
），∴
=
，∴OB=2，∴B（－2，0）．∵抛物线过点A，B，∴
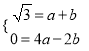，解得：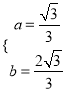 
，∴
；
（2）抛物线的对称轴为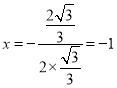
．∵点B与点O关于对称轴
对称，∴由题意得直线AB与对称轴的交点就是点M．设直线AB为： 
．∵直线AB过A、B两点，∴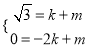
，解得： 
，∴
．
当
时， 
，∴M（
， 
）；
（3）设F（x，0），则E（x， 
），P（x， 
），则PE=
，整理得： 
，∴
或
，解得：x1=0，x2=-1，x3=
，x4=
．∴E的坐标为（0， 
）或（
， 
）或（
， 
）或（
， 
）．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
