题目内容
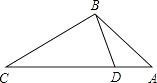
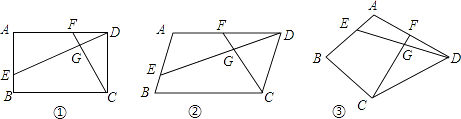
【题目】如图,在△ABC中,∠ABC的平分线BF与△ABC的外角平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E。

(1)写出图中所有的等腰三角形,并选择其中一个说明理由。
(2)直接写出BD,CE,DE之间的数量关系。
(3)若DE=5cm,CE=8cm,BF=24cm,求△BDF的面积。
【答案】(1)详见解析;(2)BD=DE+CE;(3)60.
【解析】试题分析:(1)根据已知条件,BF、CF分别平分∠ABC、∠ACB的外角,且DE∥BC,可得∴∠DBF=∠DFB,∠ECF=∠EFC,因此可判断出△BDF和△CEF为等腰三角形;
(2)由(1)可得出DF=BD,CE=EF,所以得BD-CE=DE;
(3)作BF边上的高,由勾股定理得到高为5,计算得到△BDF的面积为60.
试题解析:(1)△DBF、△ECF
以说明△DBF为例:
∵BF平分∠ABC
∴∠DBF=∠CBF
∵DF∥BC
∴∠CBF=∠DFB
∴∠DBF=∠DFB,
即△DBF为等腰三角形;
(2)存在:BDCE=DE,
证明:∵DF=BD,CE=EF,
∴BDCE=FDEF=DE.
(3)作DM⊥BF与点M,
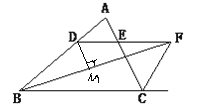
由(1)知△DBF为等腰三角形,
∴BM=![]() BF=12cm,
BF=12cm,
由(2)知BD=DE+EC=5+8=13cm,
由勾股定理,得DM=![]() =5cm,
=5cm,
S△BDF=![]() ×BF×DM=
×BF×DM=![]() ×24×5= 60(cm2)
×24×5= 60(cm2)

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目