题目内容
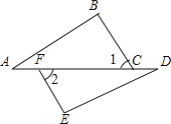
【题目】已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.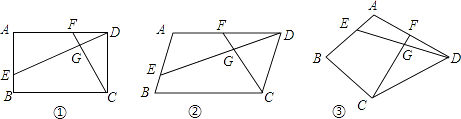
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证:△ADE∽△DCF;
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时, ![]() 成立?并证明你的结论;
成立?并证明你的结论;
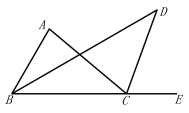
(3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,请直接写出 ![]() 的值.
的值.
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∴∠ADE+∠CDG=90°,
又∵DE⊥CF,∠CDG+∠DCF=90°,
∴∠ADE=∠DCF,
∴△ADE∽△DCF.
(2)
解:当∠B+∠EGC=180°时, ![]() 成立,理由如下:
成立,理由如下:
在AD的延长线上取点M,使CM=CF,如图1所示:
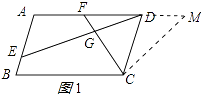
则∠CMF=∠CFM.∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠A=∠CDM,∠FCB=∠CFM,
∵∠B+∠EGC=180°,
∴∠BEG+∠FCB=360°﹣(∠B+∠EGC)=180°,
又∵∠BEG+∠AED=180°,
∴∠AED=∠FCB,
∴∠CMF=∠AED.
∴△ADE∽△DCM,
∴ ![]() ,
,
∴ ![]() ;
;
(3)
解: ![]() ;理由如下:
;理由如下:
连接AC、BD,交于点M,作CN⊥AD于N,如图2所示:

∵∠BAD=90°,AB=6,AD=8,
∴BD= ![]() =
= ![]() =10,
=10,
在△ABD和△CBD中, 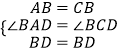 ,
,
∴△ABD≌△CBD(SAS),
∴∠ABD=∠CBD,
∵AB=CB,
∴BD⊥AC,AM=CM,
∴∠AMD=90°=∠BAD,
又∵∠ADB=∠MDA,
∴△ABD∽△MAD,
∴AD:DM=BD:AD,
∴AD2=BDDM,即82=10DM,
∴DM=6.4,
∴AM= ![]() =
= ![]() =4.8,
=4.8,
∴AC=2AM=9.6,
∵△ACD的面积= ![]() ADCN=
ADCN= ![]() ACDM,
ACDM,
∴8×CN=9.6×6.4,
解得:CN=7.68,
∵DE⊥CF,
∴∠CFN=∠DAE,
∵CN⊥AD,
∴∠CNF=90°=∠DAE,
∴△ADE∽△NCF,
∴ ![]() =
= ![]() =
= ![]() .
.
【解析】(1)由矩形的性质得出∠A=∠ADC=90°,由角的互余关系整除∠ADE=∠DCF,即可得出△ADE∽△DCF;(2)在AD的延长线上取点M,使CM=CF,由等腰三角形的性质得出∠CMF=∠CFM.由平行四边形的性质得出∠A=∠CDM,∠FCB=∠CFM,证出∠BEG+∠FCB=180°,得出∠AED=∠FCB,因此∠CMF=∠AED.证明△ADE∽△DCM,得出对应边成比例 ![]() ,即可得出结论;(3)连接AC、BD,交于点M,作CN⊥AD于N,由勾股定理求出BD,由SAS证明△ABD≌△CBD,得出∠ABD=∠CBD,由等腰三角形的性质得出AM=CM,∠AMD=90°=∠BAD,证明△ABD∽△MAD,得出对应边成比例求出DM,由勾股定理求出AM,由△ACD的面积求出CN,证明△ADE∽△NCF,得出对应边成比例,即可得出结果.
,即可得出结论;(3)连接AC、BD,交于点M,作CN⊥AD于N,由勾股定理求出BD,由SAS证明△ABD≌△CBD,得出∠ABD=∠CBD,由等腰三角形的性质得出AM=CM,∠AMD=90°=∠BAD,证明△ABD∽△MAD,得出对应边成比例求出DM,由勾股定理求出AM,由△ACD的面积求出CN,证明△ADE∽△NCF,得出对应边成比例,即可得出结果.
【考点精析】关于本题考查的等腰三角形的性质,需要了解等腰三角形的两个底角相等(简称:等边对等角)才能得出正确答案.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案