题目内容
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y= ![]() (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.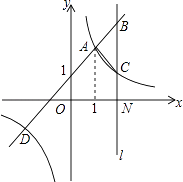
(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
【答案】
(1)
解:∵反比例函数经过点D(﹣2,﹣1),
∴把点D代入y= ![]() (m≠0),
(m≠0),
∴﹣1= ![]() ,
,
∴m=2,
∴反比例函数的解析式为:y= ![]() ,
,
∵点A(1,a)在反比例函数上,
∴把A代入y= ![]() ,得到a=
,得到a= ![]() =2,
=2,
∴A(1,2),
∵一次函数经过A(1,2)、D(﹣2,﹣1),
∴把A、D代入y=kx+b (k≠0),得到: ![]() ,
,
解得: ![]() ,
,
∴一次函数的解析式为:y=x+1;
(2)
解:据图可知:当﹣2<x<0或x>1时,一次函数的值大于反比例函数的值;
(3)
解:过点A作AE⊥x轴交x轴于点E,
∵直线l⊥x轴,N(3,0),
∴设B(3,p),C(3,q),
∵点B在一次函数上,
∴p=3+1=4,
∵点C在反比例函数上,
∴q= ![]() ,
,
∴S△ABC= ![]() BCEN=
BCEN= ![]() ×(4﹣
×(4﹣ ![]() )×(3﹣1)=
)×(3﹣1)= ![]() .
.
【解析】(1)由反比例函数经过点D(﹣2,﹣1),即可求得反比例函数的解析式;然后求得点A的坐标,再利用待定系数法求得一次函数的解析式;(2)结合图象求解即可求得x在什么范围内,一次函数的值大于反比例函数的值;(3)首先过点A作AE⊥x轴交x轴于点E,由直线l与x轴垂直于点N(3,0),可求得点E,B,C的坐标,继而求得答案.

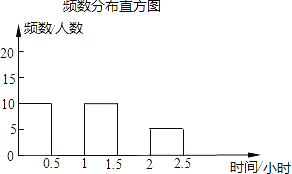
【题目】(根据市教委提出的学生每天体育锻炼不少于1小时的要求,为确保阳光体育运动时间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:
时间分组(小时) | 频数(人数) | 频率 |
0≤t<0.5 | 10 | 0.2 |
0.5≤t<1 | 0.4 | |
1≤t<1.5 | 10 | 0.2 |
1.5≤t<2 | 0.1 | |
2≤t<2.5 | 5 | |
合计 | 1 |
请你将频数分布表和频数分布直方图补充完整.