题目内容
【题目】已知△ABC中,AB=AC,CD⊥AB于D.
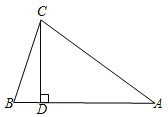
(1)若∠A=38,求∠DCB的度数;
(2)若AB=5,CD=3,求BC的长.
【答案】(1)19°,(2)![]() .
.
【解析】
试题分析:(1)在△ABC中,AB=AC,∠A=38°,利用等腰三角形的性质求出∠B的度数,在Rt△CBD中,求出∠DCB的度数;
(2)在Rt△CDA中,利用勾股定理求出AD的长,然后求出BD的长,最后在Rt△CBD中,利用勾股定理求出CB的长度.
试题解析:(1)∵在△ABC中,AB=AC,∠A=38°,
∴∠B=![]() (180°-38°)=71°,
(180°-38°)=71°,
又∵CD⊥AB于D,
∴在Rt△CBD中,∠DCB=90°-∠B=19°,
(2)在Rt△CDA中,
∵AC=AB=5,CD=3,
∴AD=![]() =4,
=4,
∴BD=AB-AD=5-4=1,
在Rt△CBD中,BC=![]() .
.

练习册系列答案
相关题目
【题目】某瓜农采用大棚栽培技术种植了一亩地的良种西瓜,这亩地产西瓜600个,在西瓜上市前该瓜农随机摘下了10个成熟的西瓜,称重如下:
西瓜质量(单位:千克) | 5.4 | 5.3 | 5.0 | 4.8 | 4.4 | 4.0 |
西瓜数量(单位:个) | 1 | 2 | 3 | 2 | 1 | 1 |
(1)这10个西瓜质量的众数和中位数分别是 和 ;
(2)计算这10个西瓜的平均质量,并根据计算结果估计这亩地共可收获西瓜约多少千克?
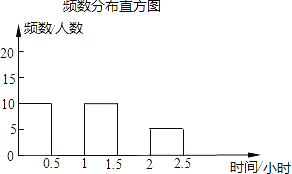
【题目】(根据市教委提出的学生每天体育锻炼不少于1小时的要求,为确保阳光体育运动时间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:
时间分组(小时) | 频数(人数) | 频率 |
0≤t<0.5 | 10 | 0.2 |
0.5≤t<1 | 0.4 | |
1≤t<1.5 | 10 | 0.2 |
1.5≤t<2 | 0.1 | |
2≤t<2.5 | 5 | |
合计 | 1 |
请你将频数分布表和频数分布直方图补充完整.