题目内容
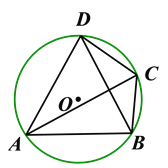
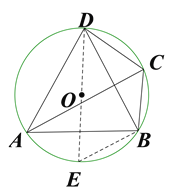
【题目】如图,在⊙O的内接四边形ABCD中,∠BCD=120°,AC平分∠BCD.
(1)求证:△ABD是等边三角形;
(2)若BD=6cm,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】【试题分析】(1)因为AC平分∠BCD,∠BCD=120°, 根据角平分线的定义得:∠ACD=∠ACB=60°. 根据同弧所对的圆周角相等,得∠ACD=∠ABD, ∠ACB=∠ADB , ∠ABD=∠ADB=60°.根据三个角是60度的三角形是等边三角形得,△ABD是等边三角形.
(2)作直径DE,连结BE ,由于△ABD是等边三角形,则∠BAD=60°同弧所对的圆周角相等,得∠BED=∠BAD=60°.因为DE是直径,根据直径所对的圆周角是直角得,∠EBD=90°.
则∠EDB=30°,30度所对的直角边是斜边的一半,得DE=2BE .
设EB=x,则ED=2x,根据勾股定理得,(2x)2-x2=62.
解得: ![]() ,即
,即![]() .
.
【试题解析】
(1)∵AC平分∠BCD,∠BCD=120° ,
∴∠ACD=∠ACB=60°.
∵∠ACD=∠ABD, ∠ACB=∠ADB .
∴∠ABD=∠ADB=60°.
∴△ABD是等边三角形.
(2)作直径DE,连结BE
∵△ABD是等边三角形,
∴∠BAD=60°
∴∠BED=∠BAD=60°
∵DE是直径,
∴∠EBD=90°.
∴∠EDB=30°.
∴DE=2BE .
设EB=x,则ED=2x,
∴(2x)2-x2=62.
∵x>0.
∴![]() .
.
∴![]()
即![]() .
.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目