题目内容
【题目】△ABC是一个三角形的纸片,点D,E分别是△ABC边AB,AC上的两点.
(1)如图①,如果沿直线DE折叠,则∠BDA′与∠A的关系是____________;
(2)如果折成图②的形状,猜想∠BDA′,∠CEA′和∠A的关系,并说明理由;
(3)如果折成图③的形状,猜想∠BDA′,∠CEA′和∠A的关系,并说明理由.
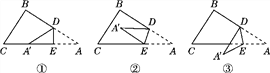
【答案】(1)∠BDA′=2∠A;(2)∠BDA′+∠CEA′=2∠A,理由见解析;(3)∠BDA′-∠CEA′=2∠A,理由见解析.
【解析】试题分析:(1)由折叠可得∠DA′A=∠A,根据三角形外角的性质可得∠BDA′=∠DA′A+∠A =2∠A;(2)∠BDA′+∠CEA′=2∠A,在四边形ADA′E中,根据四边形的内角和为360°可得∠A+∠A′+∠ADA′+∠A′EA=360°,即∠A+∠A′=360°-∠ADA′-∠A′EA.又因∠BDA′+∠ADA′=180°,∠CEA′+∠A′EA=180°,所以∠BDA′+∠CEA′=360°-∠ADA′-∠A′EA,即可得∠BDA′+∠CEA′=∠A+∠A′.再由折叠的性质可得∠A=∠A′,所以∠BDA′+∠CEA′=2∠A.(3)∠BDA′-∠CEA′=2∠A,设DA′交AC于点F,根据三角形外角的性质可得∠BDA′=∠A+∠DFA,∠DFA=∠A′+∠CEA′,即可得∠BDA′=∠A+∠A′+∠CEA′,所以∠BDA′-∠CEA′=∠A+∠A′.再由折叠的性质可得∠A=∠A′,所以∠BDA′-∠CEA′=2∠A.
试题解析:
(1)∠BDA′=2∠A
(2)∠BDA′+∠CEA′=2∠A,
理由:∵在四边形ADA′E中,
∠A+∠A′+∠ADA′+∠A′EA=360°,
∴∠A+∠A′=360°-∠ADA′-∠A′EA.
∵∠BDA′+∠ADA′=180°,∠CEA′+∠A′EA=180°,
∴∠BDA′+∠CEA′=360°-∠ADA′-∠A′EA,
∴∠BDA′+∠CEA′=∠A+∠A′.
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠A′,∴∠BDA′+∠CEA′=2∠A.
(3)∠BDA′-∠CEA′=2∠A.
理由:设DA′交AC于点F,
∵∠BDA′=∠A+∠DFA,∠DFA=∠A′+∠CEA′,
∴∠BDA′=∠A+∠A′+∠CEA′,
∴∠BDA′-∠CEA′=∠A+∠A′.
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠A′,
∴∠BDA′-∠CEA′=2∠A.