题目内容
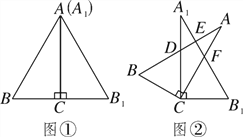
【题目】将两块相同的含30°角的直角三角板按图①的方式放置,已知∠BAC=∠B1A1C=30°,AB=2BC.固定三角板A1B1C,然后将三角板ABC绕点C顺时针方向旋转至图②的位置,AB与A1C、A1B1分别交于点D、E,AC与A1B1交于点F.
(1)当旋转角等于20°时,∠BCB1=________度;
(2)当旋转角等于多少度时,AB与A1B1垂直?请说明理由.
【答案】(1)160°,(2)见解析
【解析】试题分析:(1)根据旋转的性质可得∠ACA1=20°,再根据直角三角形两锐角互余求出∠BCD,然后根据∠BCB1=∠BCD+∠A1CB1进行计算即可得解;
(2)根据直角三角形两锐角互余求出∠A1DE,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠ACA1,即为旋转角的度数.
试题解析:(1)由旋转的性质得,∠ACA1=20°,
∴∠BCD=∠ACB-∠ACA1=90°-20°=70°,
∴∠BCB1=∠BCD+∠A1CB1,
=70°+90°,
=160°;
(2)∵AB⊥A1B1,
∴∠A1DE=90°-∠B1A1C=90°-30°=60°,
∴∠ACA1=∠A1DE-∠BAC=60°-30°=30°,
∴旋转角为30°.

练习册系列答案
相关题目