题目内容
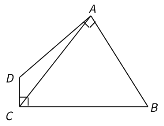
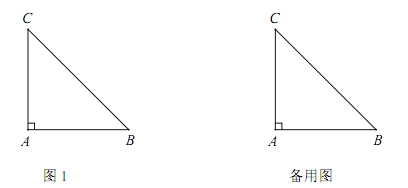
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
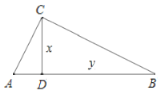
,![]() ,为了研究图中线段之间的关系,设
,为了研究图中线段之间的关系,设![]() ,
,![]() ,
,
(1)可通过证明![]() ,得到
,得到![]() 关于
关于![]() 的函数表达式
的函数表达式![]() __________,其中自变量
__________,其中自变量![]() 的取值范围是___________;
的取值范围是___________;
(2)根据图中给出的(1)中函数图象上的点,画出该函数的图象;

(3)借助函数图象,回答下列问题:①![]() 的最小值是__________;②已知当
的最小值是__________;②已知当![]() 时,
时,![]() 的形状与大小唯一确定,借助函数图象给出
的形状与大小唯一确定,借助函数图象给出![]() 的一个估计值(精确到0.1)或者借助计算给出
的一个估计值(精确到0.1)或者借助计算给出![]() 的精确值.
的精确值.
【答案】(1)![]() ,x>1;(2)见解析;(3)k≈6.5或k≈-0.5
,x>1;(2)见解析;(3)k≈6.5或k≈-0.5
【解析】
(1)利用相似边之间的关系,可求得x、y之间的关系,结合实际情况,AD>0可得到x的取值范围;
(2)描点绘制函数曲线;
(3)①直接读图可得到;
(3)②△ABC的形状要想唯一,则当k为某一个值时,x、y的值必须为唯一值.x是y的函数,只要x的值唯一,则y的值必定唯一.故只需要将k代入求解,使得x的值为唯一即可
(1)∵∠ACB=90°,CD⊥AB
∴∠A+∠ACD=90°,∠ACD+∠DCB=90°
∴∠A=∠DCB
∵∠ADC=∠CDB=90°
∴△ACD∽△CBD
∵CD-AD=1,CD=x,∴AD=x-1
∴![]() ,代入化简得:y=
,代入化简得:y=![]()
∵AD>0,∴x-1>0,x>1
(2)连接这些点,绘制函数图形如下:
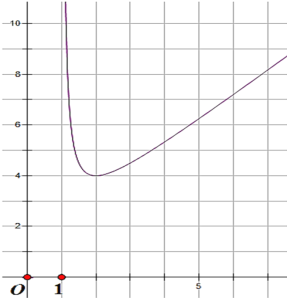
(3)①,由第(2)问的图形可得,y的最小值为4;
(3)②∵AB+CD=k,∴x-1+y+x=k
∵y=![]() ,代入得:2x-1+
,代入得:2x-1+![]() =k,化简得:
=k,化简得:![]()
∵要使△ABC的图形唯一,则需要使得x、y的值唯一
∴上述以x为未知数的一元二次方程的有一个解
∴△=![]() ,化简得:
,化简得:![]()
解得:k=3±![]()
∴k≈6.5或k≈-0.5

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目