题目内容
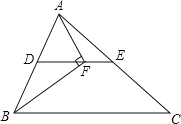
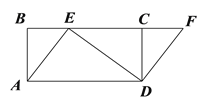
【题目】如图,四边形ABCD是矩形,点E在BC边上,点F在BC延长线上,且∠CDF =∠BAE.
(1)求证:四边形AEFD是平行四边形;
(2)若DF=3,DE=4,AD=5,求CD的长度.
【答案】(1)见解析;(2)![]() .
.
【解析】分析:(1)直接利用矩形的性质结合全等三角形的判定与性质得出BE=CF,进而得出答案;
(2)利用勾股定理的逆定理得出∠EDF=90 ,进而得出![]() ED·DF=
ED·DF=![]() EF·CD,求出答案即可.
EF·CD,求出答案即可.
详解:(1)∵四边形ABCD是矩形,
∴AB=CD, ∠B=∠DCF=90.
∵![]() ,
,
∴△ABE≌△DCF.
∴BE=CF,
∴BC=EF.
∵BC=AD, ∴EF=AD.又∵EF∥AD,
∴四边形AEFD是平行四边形.
(2)解:由(1)知,EF=AD= 5.
在△EFD中,DF=3,DE=4,EF=5,
∴![]() .
.
∴∠EDF=90.
∴![]() EDDF=
EDDF=![]() EFCD,
EFCD,
∴CD=![]() .
.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目