Question

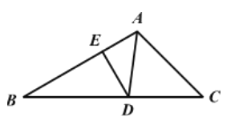
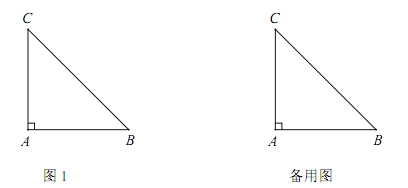
【题目】如图，在△ABC中，∠BAC=90°，AB=AC，点P为线段AC上一点，点Q在线段AB的延长线上，CP=BQ，连接PQ交BC于点D，点P关于BC的对称点为E，连接AE．

（1）依题意补全图1；

（2）求证：D是PQ的中点；

（3）用等式表示AE和PQ的数量关系，并证明．

Answer 1

【答案】（1）见解析；（2）见解析；（3），理由见解析

【解析】

（1）根据题意画图即可；

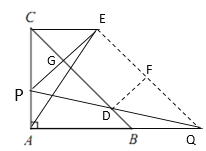
（2）连接EQ，过点D作DF⊥EQ，设PE及哦啊BC于点G，先证四边形CEQB是平行四边形，得到BC∥EQ，再求∠PEQ=90°得到四边形EGDF是矩形，根据对称证得DF=PE，得到DF是△PEQ的中位线，由此得到结论；

（3）设AP=a，PC=CE=b，利用勾股定理求出，，即可得到结论.

（1）如图：

（2）连接EQ，过点D作DF⊥EQ，设PE交BC于点G，

∵AB=AC，∠BAC=90°，

∴∠ACB=∠ABC=45°，

∵点P关于BC的对称点为E，

∴∠BCE=∠ACB=∠ABC=45°，PC=CE，

∴CE∥AB，

∵BQ=PC=CE，

∴四边形CEQB是平行四边形，

∴BC∥EQ，

∴∠CEQ=∠CBQ=180°-45°=135°，

∵∠PCE=45°+45°=90°，PC=CE，

∴∠CEP=45°，

∴∠PEQ=90°，即PE⊥EQ，

∵DF⊥EQ，

∴PE∥DF，

∴四边形EGDF是平行四边形，

∵∠GEF=90°，

∴四边形EGDF是矩形，

∴DF=EG,

由对称得PG=EG，

∴DF=PE，

∴DF是△PEQ的中位线，

∴点D是PQ的中点；

（3）；

设AP=a，PC=CE=b，

在Rt△ACE中，,

∴；

在Rt△PEQ中，，

∵， ，

∴，

∴,

∴.