Question

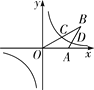
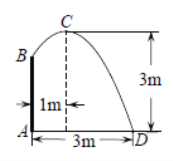
【题目】如图，在喷水池的中心处竖直安装一根水管，水管的顶端安有一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高点，高度为3m，水柱落地点离池中心处3m，以水平方向为轴，建立平面直角坐标系，若选取点为坐标原点时的抛物线的表达式为，则选取点为坐标原点时的抛物线表达式为______，其中自变量的取值范围是______，水管的长为______m．

Answer 1

【答案】y＝（x＋2）2＋3 3≤x≤0 2.25

【解析】

直接利用二次函数的平移规律进而得出答案，再由题意可得，x＝3时得到的y值即为水管的长．

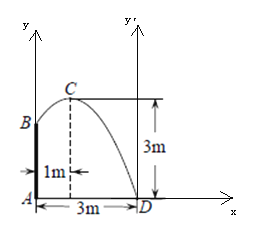
以池中心A为原点，竖直安装的水管为y轴，与水管垂直的为x轴建立直角坐标系．

抛物线的解析式为，

当选取点D为坐标原点时，相当于将原图象向左平移3个单位，

故平移后的抛物线表达式为：（3≤x≤0）；

令x＝3，则y＝＋3＝2.25．

故水管AB的长为2.25m．

故答案为：y＝（x＋2）2＋3；3≤x≤0；2.25．