��Ŀ����
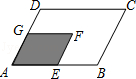
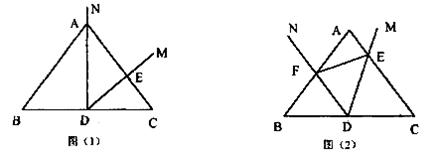
��ͼ����֪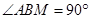 ��AB��AC������A��AG��BC������ΪG���ӳ�AG��BM��D������A��AN��BM������C��EF��AD��������AN��BM�ֱ��ཻ�ڵ�F��E��
��AB��AC������A��AG��BC������ΪG���ӳ�AG��BM��D������A��AN��BM������C��EF��AD��������AN��BM�ֱ��ཻ�ڵ�F��E��
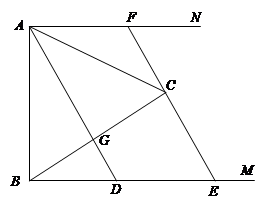
��1����֤����BCE�ס�AGC��
��2����P������AD�ϵ�һ�����㣬��AP��x���ı���ACEP�������y����AF��5��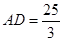 ��
��
����y����x�ĺ�����ϵʽ����д��������
�ڵ���P������AD���˶�ʱ���Ƿ���������ĵ�P��ʹ�á�CPE���ܳ�Ϊ��С�������ڣ������ʱy��ֵ���������ڣ���˵�����ɡ�
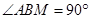 ��AB��AC������A��AG��BC������ΪG���ӳ�AG��BM��D������A��AN��BM������C��EF��AD��������AN��BM�ֱ��ཻ�ڵ�F��E��
��AB��AC������A��AG��BC������ΪG���ӳ�AG��BM��D������A��AN��BM������C��EF��AD��������AN��BM�ֱ��ཻ�ڵ�F��E��
��1����֤����BCE�ס�AGC��
��2����P������AD�ϵ�һ�����㣬��AP��x���ı���ACEP�������y����AF��5��
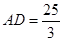 ��
������y����x�ĺ�����ϵʽ����д��������
�ڵ���P������AD���˶�ʱ���Ƿ���������ĵ�P��ʹ�á�CPE���ܳ�Ϊ��С�������ڣ������ʱy��ֵ���������ڣ���˵�����ɡ�
��1����EF��AD�ɵá�AGC=��BCE����AB=AC�ɵá�ABC=��ACB���ٸ���ͬ�ǵ������ȿɵá�ACB=��BEC������֤�ý��ۣ�
��2��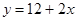 ��x��0����
��x��0����
��3������P�˶�����Dʱ��B��P��E���㹲��ʱ���ܳ���СΪ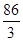
��2��
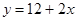 ��x��0����
��x��0������3������P�˶�����Dʱ��B��P��E���㹲��ʱ���ܳ���СΪ
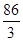
�����������1����EF��AD�ɵá�AGC=��BCE����AB=AC�ɵá�ABC=��ACB���ٸ���ͬ�ǵ������ȿɵá�ACB=��BEC������֤�ý��ۣ�
��2��������ɵ��ı���ACEPΪ���Σ��������ε������ʽ���ɵõ������
��3����ͼ�ɵõ���P�˶�����Dʱ��B��P��E���㹲��ʱ�ܳ���С�����ݹ��ɶ���������ý��.
��1����EF��AD
���AGC=��BCE����ADB=��BEC
��AB=AC
���ABC=��ACB
��
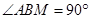 ��AG��BC
��AG��BC���ABC+��GBD=90�㣬��ADB+��GBD=90��
���ABC=��ADB
���ACB=��BEC
���BCE�ס�AGC��
��2����������ı���ACEPΪ����
��y����x�ĺ�����ϵʽΪ
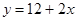 ��x��0����
��x��0������3����ͼ�ɵõ���P�˶�����Dʱ��B��P��E���㹲��ʱ���ܳ���СΪ
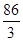 .
.���������������Ӧ���dz�����ѧ���ص���ѵ㣬���п����ȵ㣬������ѹ�����м�Ϊ������Ҫ�ر�ע��.

��ϰ��ϵ�д�
�����Ŀ
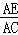 =
= =
=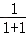 ʱ����
ʱ����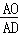 =
=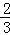 =
=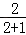 ��
��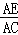 =
= =
=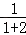 ʱ����
ʱ����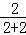 ��
��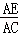 =
=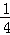 =
=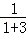 ʱ����
ʱ����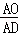 =
=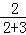 ��������
��������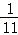 ʱ��
ʱ��

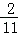
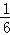
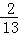
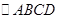 �У��Խ���
�У��Խ���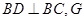 ΪBD�ӳ�����һ����
ΪBD�ӳ�����һ����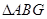 Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�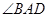 ��
��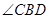 ��ƽ�����ཻ�ڵ�
��ƽ�����ཻ�ڵ�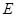 ������
������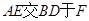 ������
������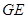 ��
��
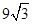 ����
����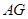 �ij���
�ij���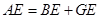 ��
��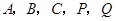 ���ף��ң����������Ƿ���ֽ�еĸ�㣬Ϊʹ
���ף��ң����������Ƿ���ֽ�еĸ�㣬Ϊʹ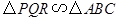 �����
����� Ӧ�Ǽף��ң��������ĵ��еģ� ����
Ӧ�Ǽף��ң��������ĵ��еģ� ����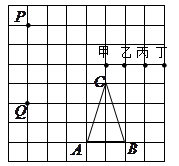
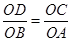 ��
��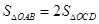 . ������ȷ�Ľ����ǣ� ��
. ������ȷ�Ľ����ǣ� ��