题目内容
在△ABC中,AB=AC,D为BC边中点,以点D为顶点作∠MDN=∠B。
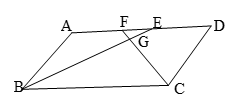
(1)当射线DN经过点A时,DM交AC边于点E,如图(1),不添加辅助线,直接写出图中所有与△ADE相似的三角形(不需要证明);
(2)将∠MDN绕点D沿逆时针方向旋转,DM、DN分别交线段AC、AB于点E、F(点E与点A不重合,如图(2))。
①求证:△BDF~△CED;②△BDF与△DEF是否相似?并证明你的结论。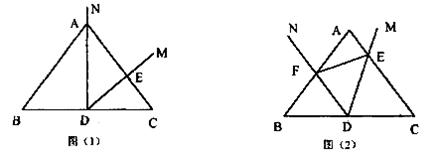
(1)当射线DN经过点A时,DM交AC边于点E,如图(1),不添加辅助线,直接写出图中所有与△ADE相似的三角形(不需要证明);
(2)将∠MDN绕点D沿逆时针方向旋转,DM、DN分别交线段AC、AB于点E、F(点E与点A不重合,如图(2))。
①求证:△BDF~△CED;②△BDF与△DEF是否相似?并证明你的结论。

通过三角形的相似来分析求证
试题分析:(1)与△ADE相似的三角形有△ABD、△ACD、△DCE。 3分
(2)①证明:
∵∠BFD=180°-∠B-∠BDF,∠EDC=180°-∠EDF-∠BDF
∴∠BFD=∠EDC 5分
∵AB=AC ∴∠B=∠C
∴△BDF∽△CED 7分
②△BDF∽△DEF 8分
证明:∵△BDF∽△CED
∴
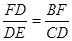 9分
9分∵BD=CD
∴
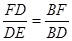 ∴
∴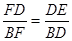 10分
10分又∠EDF=∠B
∴△BDF∽△DEF
点评:相似三角形的判定基本方法是:如果一个三角形的两个角与另一个三角形的对应角相等;如果两个三角形的两组边对应成比例,且夹角对应相等;平行于三角形一边的直线截其它两边所在的直线,截得的三角形与原三角形相似

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
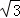 :1
:1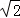 :1
:1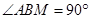 ,AB=AC,过点A作AG⊥BC,垂足为G,延长AG交BM于D,过点A做AN∥BM,过点C作EF∥AD,与射线AN、BM分别相交于点F、E。
,AB=AC,过点A作AG⊥BC,垂足为G,延长AG交BM于D,过点A做AN∥BM,过点C作EF∥AD,与射线AN、BM分别相交于点F、E。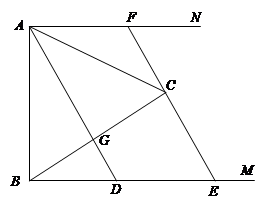
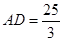 。
。
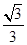 x+
x+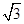 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )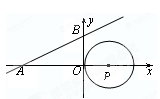
 中,
中,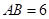 cm ,
cm ,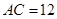 cm ,动点
cm ,动点 以1cm/s 的速度从点
以1cm/s 的速度从点 出发到点
出发到点 止,动点
止,动点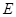 以2cm/s 的速度从点
以2cm/s 的速度从点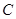 出发到点
出发到点