题目内容
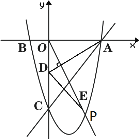
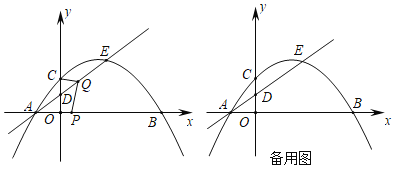
【题目】如图,在平面直角坐标系中,抛物线y=ax2+x+c与直线![]() 交于点A和点E,点A在x轴上.抛物线y=ax2+x+c与x轴另一个交点为点B,与y轴交于点C(0,
交于点A和点E,点A在x轴上.抛物线y=ax2+x+c与x轴另一个交点为点B,与y轴交于点C(0,![]() ),直线
),直线![]() 与y轴交于点D.
与y轴交于点D.
(1)求点D的坐标和抛物线y=ax2+x+c的函数表达式;
(2)动点P从点B出发,沿x轴以每秒2个单位长度的速度向点A运动,动点Q从点A出发沿射线AE以每秒1个单位长度的速度向点E运动,当点P到达点A时,点P、Q同时停止运动.设运动时间为t秒,连接AC、CQ、PQ.
①当△APQ是以AP为底边的等腰三角形时,求t的值;
②在点P、Q运动过程中,△ACQ的面积记为S1,△APQ的面积记为S2,S=S1+S2,当S=![]() 时,请直接写出t的值.
时,请直接写出t的值.
【答案】(1)抛物线的函数表达式为![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)根据题意首先求出A、D的坐标,再利用待定系数法即可解决问题;
(2)①如图1,过点Q作QF⊥AP于点F,则AF=PF=![]() AP=
AP=![]() (5﹣2t),AQ=t,证得OD∥QF,得出
(5﹣2t),AQ=t,证得OD∥QF,得出![]() ,可求出t的值;
,可求出t的值;
②如图2,过点C作CM⊥AQ于点M,过点Q作QN⊥x轴于点N,证明△AOD∽△CMD,求出CM,则S1可用t表示,证明△AOD∽△AQN,求出QN,则S2可用t表示,则可得出t的方程,解方程即可得出答案.
解:(1)∵直线![]() 与y轴交于点D,
与y轴交于点D,
∴x=0时,y=![]() ,
,
∴D(0,![]() ),
),
∵直线![]() 与x轴交于点A,
与x轴交于点A,
∴y=0时,![]() =0,
=0,
∴x=﹣1,
∴A(﹣1,0),
∵抛物线y=ax2+x+c经过点A(﹣1,0),C(0,![]() ),
),
∴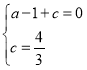 ,
,
解得: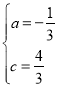 ,
,
∴抛物线的函数表达式为![]() ;
;
(2)①如图1,过点Q作QF⊥AP于点F,
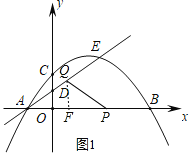
若AQ=PQ,则AF=PF=![]() AP=
AP=![]() (5﹣2t),AQ=t,
(5﹣2t),AQ=t,
∵OD⊥AP,QF⊥AP,
∴OD∥QF,
∴![]() ,
,
∵D(0,![]() ),A(﹣1,0),
),A(﹣1,0),
∴OD=![]() ,AO=1,
,AO=1,
∴AD=![]() =
=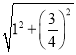 =
=![]() ,
,
∴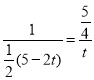 ,
,
解得:t=![]() .
.
∴t=![]() 时,△APQ是以AP为底边的等腰三角形.
时,△APQ是以AP为底边的等腰三角形.
②如图2,过点C作CM⊥AQ于点M,过点Q作QN⊥x轴于点N,
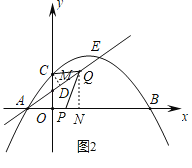
∵∠ADO=∠CDM,∠AOD=∠CMD=90°,
∴△AOD∽△CMD,
∴![]() ,
,
∵CD=OC﹣OD=![]() ,AD=
,AD=![]() ,OA=1,
,OA=1,
∴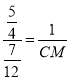 ,
,
∴CM=![]() ,
,
∴S△ACQ=S1=![]() AQ×CM=
AQ×CM=![]() =
=![]() ,
,
∵OD⊥x轴,QN⊥x轴,
∴OD∥QN,
∴△AOD∽△AQN,
∴![]() ,
,
∴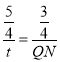 ,
,
∴QN=![]() t,
t,
∴S△APQ=S2=![]() AP×QN=
AP×QN=![]() =
=![]() ,
,
∵S1+S2=![]() ,
,
∴![]() ,
,
∴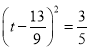 ,
,
解得:t=![]() .
.
即当S=![]() 时,t的值为
时,t的值为![]() .
.

 超能学典应用题题卡系列答案
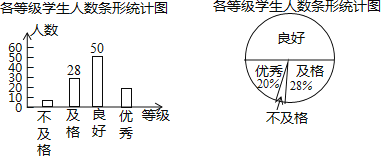
超能学典应用题题卡系列答案【题目】某学校七年级共有500名学生,为了解该年级学生的课外阅读情况,将从中随机抽取的40名学生一个学期的阅读量(阅读书籍的本数)作为样本,根据数据绘制了如下的表格和统计图:
等级 | 阅读量( | 频数 | 频率 |
E | x≤2 | 4 | 0.1 |
D | 2<x≤4 | 12 | 0.3 |
C | 4<x≤6 | a | 0.35 |
B | 6<x≤8 | c | b |
A | x>8 | 4 | 0.1 |
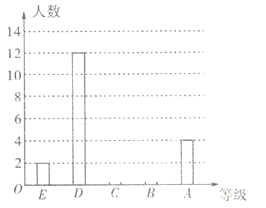
根据上面提供的信息,回答下列问题:
(1)统计表中的![]() ,
,![]() ;并补全条形统计图;
;并补全条形统计图;
(2)根据抽样调查结果,请估计该校七年级学生一学期的阅读量为“![]() 等”的有多少人?
等”的有多少人?
(3)样本中阅读量为“![]() 等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
等”的4名学生中有2名男生和2名女生,现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.