题目内容
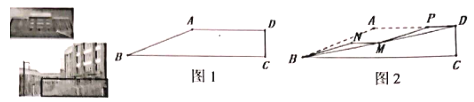
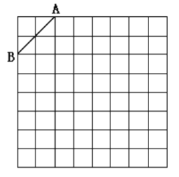
【题目】为了增加学校绿化,学校计划建造一块长为![]() 的正方形花坛
的正方形花坛![]() ,分别取四边中点
,分别取四边中点![]() ,构成四边形
,构成四边形![]() ,并计划用“两花一草”来装饰,四边形
,并计划用“两花一草”来装饰,四边形![]() 部分使用甲种花,在正方形
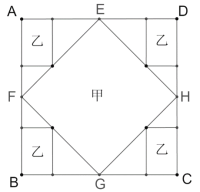
部分使用甲种花,在正方形![]() 四个角落构造4个全等的矩形区域种植乙种花,剩余部分种草坪,图纸设计如下.
四个角落构造4个全等的矩形区域种植乙种花,剩余部分种草坪,图纸设计如下.
(1)经了解,种植甲种花50元/![]() ,乙种花80元/
,乙种花80元/![]() ,草坪10元/
,草坪10元/![]() ,设一个矩形的面积为
,设一个矩形的面积为![]() ,装饰总费用为
,装饰总费用为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(2)当装饰费用为74880元时,则一个矩形区域的长和宽分别为多少?
(3)为了缩减开支,甲区域用单价为40元/![]() 的花,乙区域用单价为
的花,乙区域用单价为![]() 元/
元/![]() (
(![]() ,且
,且![]() 为10的倍数)的花,草坪单价不变,最后装饰费只用了55000元,求
为10的倍数)的花,草坪单价不变,最后装饰费只用了55000元,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)12,8;(3)50.
;(2)12,8;(3)50.
【解析】
(1)由题意,先得到四边形EFGH为正方形,然后求出面积,即可得到关系式;
(2)由(1)令y=74880,求出矩形的面积,然后利用方程,即可求出矩形的长和宽;
(3)根据题意,列出方程,然后得到![]() ,然后求出x的最大值,然后得到a的取值范围,即可得到答案.
,然后求出x的最大值,然后得到a的取值范围,即可得到答案.
解:(1)∵E,F,G,H分别为正方形ABCD各边的中点,
∴四边形EFGH为正方形,
且![]() ,
,
∴![]() ;
;
(2)令y=74880时,![]() ,
,
∴x=96
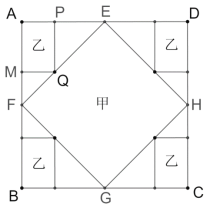
设PQ=PE=b,则AP=20-b,
∴![]() ,
,
解得:![]() ;
;
∴矩形的长为12,宽为8;
(3)由题意得![]()
∴![]()
∴![]() ,
,
∵![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
又∵a<80,且a为10的倍数,
∴a的最小值为50;

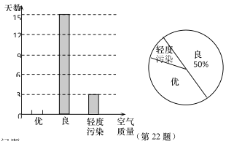
【题目】为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成如图表(成绩得分均为整数):
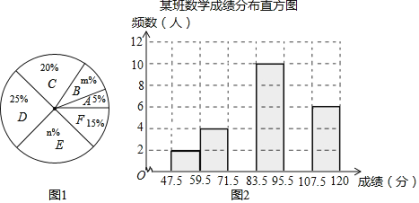
根据图表中提供的信息解答下列问题:
组别 | 成绩分组 | 频数 |
A | 47.5~59.5 | 2 |
B | 59.5~71.5 | 4 |
C | 71.5~83.5 | a |
D | 83.5~95.5 | 10 |
E | 95.5~107.5 | b |
F | 107.5~120 | 6 |
(1)频数分布表中的a= ,b= ;扇形统计图中的m= ,n= ;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 人,72分及以上为及格,预计及格的人数约为 人;
(3)补充完整频数分布直方图.