题目内容
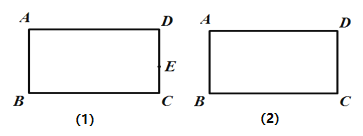
【题目】如图,四边形 ABCD 为矩形.
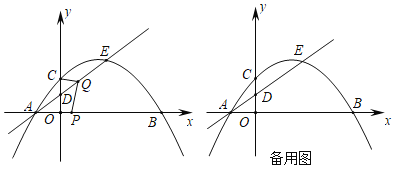
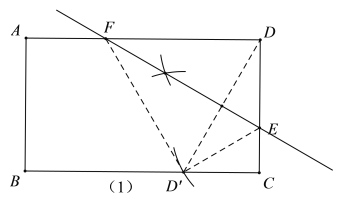
(1)如图1,E为CD上一定点,在AD上找一点F,使得矩形沿着EF折叠后,点D落在 BC边上(尺规作图,保留作图痕迹);
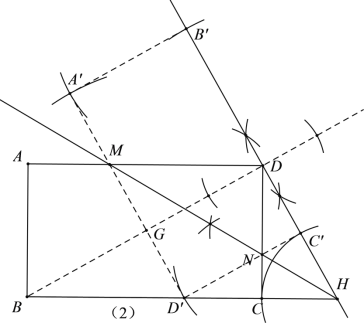
(2)如图2,在AD和CD边上分别找点M,N,使得矩形沿着MN折叠后BC的对应边B' C'恰好经过点D,且满足B' C' ⊥BD(尺规作图,保留作图痕迹);
(3)在(2)的条件下,若AB=2,BC=4,则CN= .
【答案】(1)图见解析(2)图见解析(3)![]()
【解析】
(1)以点E为圆心,以DE长为半径画弧,交BC于点D′,连接DD′,作DD′的垂直平分线交AD于点F即可;
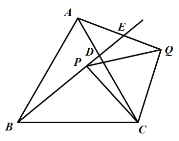
(2)先作射线BD,然后过点D作BD的垂线与BC的延长线交于点H,作∠BHD的角平分线交CD于点N,交AD于点M,在HD上截取HC′=HC,然后在射线C′D上截取C′B′=BC,此时的M、N即为满足条件的点;
(3)在(2)的条件下,根据AB=2,BC=4,即可求出CN的长.
(1)如图,点F为所求;
(2)如图,折痕MN、矩形A’B’C’D’为所求;
(3)在(2)的条件下,
∵AB=2,BC=4,
∴BD=2![]() ,
,
∵BD⊥B′C′,
∴BD⊥A′D′,
得矩形DGD′C′.
∴DG=C′D′=2,
∴BG=2![]() 2
2
设CN的长为x,CD′=y.
则C′N=x,D′N=2x,BD′=4y,
∴(4y)2=y2+(2![]() 2)2,
2)2,
解得y=![]() 1.
1.
(2x)2=x2+(![]() 1)2
1)2
解得x=![]() .
.
故答案为:![]() .
.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目