题目内容
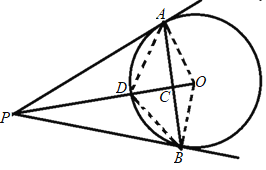
【题目】如图, 已知点P为⊙O 外一点,PA、PB是⊙O的切线,切点分别是A、B,连接OP交AB于点C,交⊙O于点D,若PA=3cm, ∠APB=60°,则下列结论正确的有( )
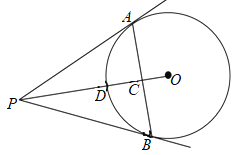
①AB⊥OP;②AC2=PC·OC;③若连接AD,BD,则∠ADB=120°;④PA,PB与劣弧AB围成的图形的面积是![]()
A.1个B.2个C.3个D.4个
【答案】D
【解析】
由切线长定理结合圆的半径相等,可得![]() 是
是![]() 的中垂线,可得结论①,
的中垂线,可得结论①,
证明![]() 可判断结论②,
可判断结论②,
证明![]() 均为等边三角形,可判断结论③,
均为等边三角形,可判断结论③,
利用PA,PB与劣弧AB围成的图形的面积等于四边形![]() 的面积减去扇形
的面积减去扇形![]() 的面积判断④.
的面积判断④.
解:连接OA,OB,则![]()
![]() PA、PB是⊙O的切线,
PA、PB是⊙O的切线,
![]()
![]() 是
是![]() 的中垂线,
的中垂线,
![]() 故①正确,
故①正确,
![]() PA是⊙O的切线,
PA是⊙O的切线,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 故②正确,
故②正确,
连接AD,BD,
![]()
![]()
![]()
![]()
![]()
![]() 是等边三角形,
是等边三角形,
![]()
同理:![]()
![]() 故③正确,
故③正确,
![]()
![]()
![]() S四边形APBO
S四边形APBO![]()
![]() 均为等边三角形,
均为等边三角形,
![]()
![]() S扇形AOBD
S扇形AOBD![]()
![]() PA,PB与劣弧AB围成的图形的面积是
PA,PB与劣弧AB围成的图形的面积是![]() .故④正确.
.故④正确.
综上:①②③④均正确,
故选D.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目