题目内容
【题目】某学校七年级共有500名学生，为了解该年级学生的课外阅读情况，将从中随机抽取的40名学生一个学期的阅读量(阅读书籍的本数)作为样本，根据数据绘制了如下的表格和统计图：
等级 | 阅读量( | 频数 | 频率 |
E | x≤2 | 4 | 0.1 |
D | 2<x≤4 | 12 | 0.3 |
C | 4<x≤6 | a | 0.35 |
B | 6<x≤8 | c | b |
A | x>8 | 4 | 0.1 |
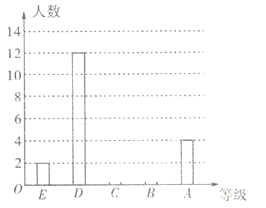
根据上面提供的信息，回答下列问题：
(1)统计表中的
，
；并补全条形统计图；
(2)根据抽样调查结果，请估计该校七年级学生一学期的阅读量为“
等”的有多少人?
(3)样本中阅读量为“等”的4名学生中有2名男生和2名女生，现从中随机挑选2名同学参加区里举行的“语文学科素养展示”活动，请用树状图法或列表法求出恰好选中“1男1女”的概率．
【答案】（1）14、0.15，补全图见解析；（2）50人；（3）
【解析】
（1）由总人数40×对应频率可求得a的值，用总频率减去其余各组的频率即可求得b的值，用总人数减去其余各组的人数即可求得c的值，进而补全条形统计图；
（2）利用七年级总人数乘以阅读量为“
等”的频率即可得解；
（3）根据列表法可求得所有等可能的情况有12种，其中恰好抽中一男一女的情况有8种，进而得解．
解：（1）由题意知
，
，
故答案为：14、0.15；
补全图形如下：
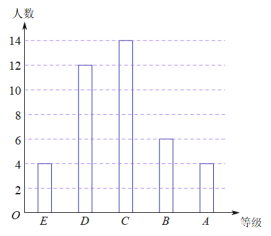
（2）估计该校七年级学生一学期的阅读量为“A等”的有500×0.1＝50（人）；
（4）列表如下：
男1 | 男2 | 女1 | 女2 | |
男1 | （男1，男2） | （男1，女1） | （男1，女2） | |
男2 | （男2，男1） | （男2，女1） | （男2，女2） | |
女1 | （女1，男1） | （女1，男2） | （女1，女2） | |
女2 | （女2，男1） | （女2，男2） | （女2，女1） |
得到所有等可能的情况有12种，其中恰好抽中一男一女的情况有8种，
所以恰好选到1名男生和1名女生的概率
．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
