题目内容
【题目】有两张相同的矩形纸片ABCD和A′B′C′D′,其中AB=3,BC=8.
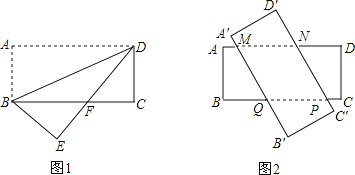
(1)若将其中一张矩形纸片ABCD沿着BD折叠,点A落在点E处(如图1),设DE与BC相交于点F,求BF的长;
(2)若将这两张矩形纸片交叉叠放(如图2),判断四边形MNPQ的形状,并证明.四边形MNPQ的最大面积是_________.(直接写出结果)
【答案】①BF=![]() ②
②![]()
【解析】试题分析:
(1)由折叠的性质结合AD∥BC易得∠FBD=∠ADB=∠FDB,由此可得BF=DF,设BF=x,结合DE=AD=BC=8,可得EF=8-x,结合BE=AB=3,在Rt△BEF中由勾股定理建立方程即可求得BF的值;
(2)①如图3,过点Q作QE⊥PN于点E,过点N过NF⊥PQ于点F,则易证△QEP≌△NFP,从而可得PQ=PN,由已知条件易证四边形MNPQ是平行四边形,两者结合即可得到四边形MNPQ是菱形;
②如图4,由题意可知,菱形MNPQ边上的高是3,故当边长越长时,面积越大,由题意可知,当点M与点A重合、点P与点C重合时,边长MQ=AQ=QC,此时面积最大,在Rt△ABQ中,由勾股定理建立方程解出MQ的长,即可求得最大面积了.
试题解析:
(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC=8,
∴∠ADB=∠DBC,
由折叠的性质可知,∠ADB=∠FDB,BE=AB=3,DE=AD=8,
∴∠DBC=∠FDB,
∴BF=DF,
设BF=x,则DF=x,
∴EF=8-x,
∵在Rt△BEF中,BF2=BE2+EF2,
∴![]() ,解得:
,解得: ![]() ;
;
(2)①如图2,四边形MNPQ是菱形,理由如下:
过点Q作QE⊥PN于点E,过点N过NF⊥PQ于点F,
∴∠PEQ=∠PFN=90°,
∵两张纸条等宽,
∴NF=QE,
∵∠NPF=∠QPE,
∴△QEP≌△NFP,
∴PQ=PN,
∵由题意可得:MN∥PQ,MQ∥NP,
∴四边形MNPQ是平行四边形,
∴四边形MNPQ是菱形;

②如图4,由题意和①可知,菱形MNPQ边上的高是3,故当菱形MNPQ的边长越长时,其面积越大,由图4可知,当点M与点A重合、点P与点C重合时,边长MQ=AQ=QC,此时面积最大,
设AQ=QP=a,则BQ=BC-QC=8-a,
∵在Rt△ABQ中,AQ2=AB2+BQ2,
∴![]() ,解得:
,解得: ![]() ,
,
∴菱形MNPQ的最大面积为: ![]() .
.


【题目】为了响应市委和市政府“绿色环保,节能减排”的号召,幸福商场用3300元购进甲、乙两种节能灯共计100只,很快售完.这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲种节能灯 | 30 | 40 |
甲种节能灯 | 35 | 50 |
(1)求幸福商场甲、乙两种节能灯各购进了多少只?
(2)全部售完100只节能灯后,商场共计获利多少元?