题目内容
【题目】如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（ 
， 
）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．
（1）求抛物线的解析式；
（2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；
（3）求△PAC为直角三角形时点P的坐标．
【答案】
（1）
解：∵B（4，m）在直线y=x+2上，
∴m=4+2=6，
∴B（4，6），
∵A（ 
， 
）、B（4，6）在抛物线y=ax2+bx+6上，
∴ 
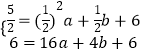，解得 
，
∴抛物线的解析式为y=2x2﹣8x+6
（2）
解：设动点P的坐标为（n，n+2），则C点的坐标为（n，2n2﹣8n+6），
∴PC=（n+2）﹣（2n2﹣8n+6），
=﹣2n2+9n﹣4，
=﹣2（n﹣ 
）2+ 
，
∵PC＞0，
∴当n= 时，线段PC最大且为
（3）
解：∵△PAC为直角三角形，
i）若点P为直角顶点，则∠APC=90°．
由题意易知，PC∥y轴，∠APC=45°，因此这种情形不存在；
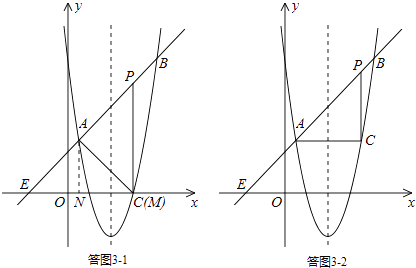
ii）若点A为直角顶点，则∠PAC=90°．
如答图3﹣1，过点A（ ， ）作AN⊥x轴于点N，则ON= ，AN= ．
过点A作AM⊥直线AB，交x轴于点M，则由题意易知，△AMN为等腰直角三角形，
∴MN=AN= ，∴OM=ON+MN= + =3，
∴M（3，0）．
设直线AM的解析式为：y=kx+b，
则：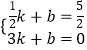 
，解得 
，
∴直线AM的解析式为：y=﹣x+3 ①
又抛物线的解析式为：y=2x2﹣8x+6 ②
联立①②式，解得：x=3或x= （与点A重合，舍去）
∴C（3，0），即点C、M点重合．
当x=3时，y=x+2=5，
∴P1（3，5）；
iii）若点C为直角顶点，则∠ACP=90°．
∵y=2x2﹣8x+6=2（x﹣2）2﹣2，
∴抛物线的对称轴为直线x=2．
如答图3﹣2，作点A（ ， ）关于对称轴x=2的对称点C，
则点C在抛物线上，且C（ 
， ）．
当x= 时，y=x+2= 
．
∴P2（ ， ）．
∵点P1（3，5）、P2（ ， ）均在线段AB上，
∴综上所述，△PAC为直角三角形时，点P的坐标为（3，5）或（ ， ）
【解析】（1）已知B（4，m）在直线y=x+2上，可求得m的值，抛物线图象上的A、B两点坐标，可将其代入抛物线的解析式中，通过联立方程组即可求得待定系数的值．（2）要弄清PC的长，实际是直线AB与抛物线函数值的差．可设出P点横坐标，根据直线AB和抛物线的解析式表示出P、C的纵坐标，进而得到关于PC与P点横坐标的函数关系式，根据函数的性质即可求出PC的最大值．（3）当△PAC为直角三角形时，根据直角顶点的不同，有三种情形，需要分类讨论，分别求解．
